см/к

см/в сек

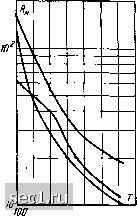Рис. 3-70, Температурная зависимость коэффициента Холла в HgTe (образцы разной степени чистоты) по [Л. 291 и 402].

гоо 300 400К

Рнс. 3-71. Температурная зависимость подвижности электронов в HgTe по [Л. 291].

см/есек

(ом-см)

см

см

Рис. 3-72. Зависимость удельной электропроводности от концентрации носителей тока в HgTe по [Л. 291, 402, 561 и 688].

Рис. 3-73. Зависимость подвижности носителей тока от нх концентрации • в HgTe по [Л. 291, 402, 561 и 688].

Измерениями Термо-Э. д. с. занимались Врач, Жданова и Лей [Л. 561], а также Гобрехт [Л. 152]. Зависимость ф от температуры и концентрации носителей приводится на рис.3-63 и 3-64. При комнатной температуре значение ф не превышает 100 мкв/град, являясь, таким образом, достаточно малым с точки зрения пригодности этого материала для изготовления датчиков Холла.

Термомагнитные явления в кристаллах HgSe изучали Цидиль-ковский (Л. 686] и Уитселт [Л. 501]. Циднльковский показал, что поперечный эффект Нернста-Эттингсгаузена, кроме зависимости от концентрации и температуры, обнаруживает сильную зависимость от магнитного поля. Результаты исследований Цидильковского приводятся на рис. 3-65 и 3-66. Уитселт подтвердил также зависимость коэффициента Риги-Ледюка от концентрации носителей и магнитного поля, что можно видеть на рис. 3-67 и 3-68.

3-7. СВОЙСТВА ТЕЛЛУРИДА РТУТИ

Теллурид ртути - второй полупроводниковый материал из группы соединений АВт - обладает свойствами, в основном, подобными свойствам HgSe, но отличается еще большими подвижностямн (наибольшее значение, полученное до настоящего времени, достигает 22 500 см/в-сек [Л. 561]) и большими значениями коэффициента Холла при несколько худших температурных свойствах. На

см->/к

10"

см

70 % 60

Рис. 3-74. Зависимость коэффициента Холла от концентрации носителей тока в HgTe по [Л. 291, 402, 561 и 688].

Рис. 3-75. Эффект магнитосопротивления в HgTe [Л. 642].

8/град-гс 1

Рис. 3-76. Температурная О

зависимость коэффициента -2

Нернста - Эттингсгаузена в -1

HgTe [Л. 687] (/, -номе- S

pa исследованных образ- S

цов). -10

/--«=(1-2) . 10" СМ-=; II -П" -(2-4) • 10" СЛ-=.

-1г -п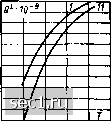

о 100 200 iOomKsoo

рис. 3-69 - 3-?4 представлены, как и в случае MgSe, основные электрические свойства HgTe, почерпнутые из многих работ [Л. 41, 73, 146, 181, 291, 401-403]. Эффект магнитосопротивления в ;><рнсталлах HgTe изучали Никольская и Регель [Л. 642]; они показали, что увеличение удельного сопротивления в поле с индукцией В=10 кгс достигает десятков процентов (рис. 3-75).

Данные о термо-э. д. с. можно найти в работе [Л. 561], где приведено значение ф=115 мкв1град при комнатной температуре.

Поперечный эффект Нернста-Эттингсгаузена изучали Цидиль-ковский [Л. 687], а также Товстюк с сотрудниками [Л. 676]. Однако результаты обеих работ не позволяют произвести корреляцию Q-L =f{n) из-за их противоречивости. Поэтому приводим только две температурные характеристики для образцов с различной концентрацией при комнатной температуре: кривая 1~п=3,9- \0" см~; кривая 11-п=2,8- 10" см- (рис. 3-76).

3-8. СИСТЕМА HgTe-HgSe

Существуют возможности получения твердых растворов системы HgTe-HgSe (например, [Л. 402]). Электрические свойства твердых растворов изменяются в зависимости от содержания Те и Se в смеси, что дает возможность изготовлять датчики Холла с промежуточными свойствами. Однако изменения эти незначительны, что

смУв-оек

гоооо

10000

Рис. 3-77. Зависимость подвижности электронов от состава твердого раствора ,в системе HgTe- HgSe [Л. 402].

HgSe

0,5 HgTe

видно из кривой зависимости подвижности носителей тока от состава, приведенной на рис. 3-77 [Л. 402]. Термоэлектрические свойства этих твердых растворов изучали Брач, Жданова н Лев [Л. 561]. Они нашли, что коэффициент ф изменяется линейно в зависимости от содержания Те, принимая значение 95 мкв/град в HgSe и 115 мкв1град в HgTe.

3-9. СИСТЕМА HgTe-CdTe

Система CdHgTe является значительно интереснее с точки зрения пригодности для изготовления датчиков Холла [Л. 137, 138, 291, 450, 614, 688].

Материал состава Cdo.iHgo.gTe имеет аномальные электрические свойства. Подвижность в нем имеет значения большие, чем в HgTe и в CdTe. Если эта аномалия при комнатной температуре проявляется в незначительной степени (рис. 3-78) [Л. 291], то при температуре 77° К подвижность достигает значений от 150 000 до 300 000 см/в-сек (рис. 3-79). При этой температуре только InSb имеет большее значение подвижности. В работе Галацки и Гирята

[Л 137] сообщается о получении материала Cdo.iHgo.gTe с примесью трллуоа со следующими свойствами при температуре Г=300 К: y„i 44,4 см/к, 0=850 {oмcм)- и .= 37 700 смЧв-сек чш ставит этот материал с точки зрения подвижности выше, чем InAs. Материал этот в настоящее время находится в стадии интенсивных

А.. см/всек

30000

Кн. см/к

80 60 40 20

20000

-10000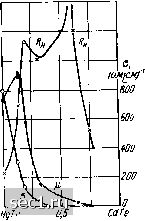

Рис. 3-78. Зависимость удельной электропроводности, коэффициента Холла и подвижности носителей тока от состава твердого раствора CdHgTe; 7=300° К [Л. 291].

т/в-сек

200000

НдТе

CdTe

Рис. 3-79.- Зависимость удельной электропроводности, коэффициента Холла и подвижности носителей тока от состава твердого раствора CdHgTe; Г=77°К

[Л. 291]: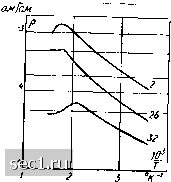

5 10

исследований, которые могут привести к дальнейшему совершенствованию электрических свойств. Следует также провести исследование возможности получения образцов напылением, чтобы проверить возможность добиться близких свойств также н в тонких слоях.

3-10. СВОЙСТВА АРСЕНИДА КАДМИЯ

Интересными электрическими свойствами обладает также недавно изученный арсенид кадмия

Рис. 3-80. Температурная зави- i"," изученный арсенид кадмия симость удельного сопротивле- CdsAso [Л. 521, 522, 523] с темпе-ния в образцах CdjAsj разной степени чистоты [Л, 521] (цифры 2, 26, 32- номера исследованных образцов).

ратурой плавления 72Г С. Он является весьма подходящим для использования в датчиках Холла, получаемых напылением, так как пленки Г13 этого материала обладают незначительноЕ! зависимостью коэффициента Холла от темпера-- туры при достаточно больших значениях подвижности (от 10О00 до 14000 см/в-сск). На рис. 3-80- 3-82 показаны основные электрические свойства этого материала, приводимые Ждановичем [Л. 521].

(м-Ул

см/всек

Рис. 3-81. Температурная зависимость коэффициента Холла в образцах CdsAsj разной степени чистоты [Л. 521] (цифры 2, 9, 26, 32-номера исследованных образцов).

100 2т 500 W 6О0°К

Рис. 3-82. Температурная зависимость подвижности носителей тока в CdaAsj [Л. 521].

мкв/ерад

-50\ -60 -70 -80 -90

300 400

Рис. 3-83. Температурная зависимость термо-э. д. с. в CdaAsa [Л. 521].

Термо-э. д. с, достигающая прн 7=300° К значения около 60 мкв/град, имеет наименьшее значение по сравнению с ранее упомянутыми полупроводниковыми материалами (рис. 3-83).

Данных о термомагнцгных эффектах в CdsAsE до сих пор нет.

Глеев четвертая

ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК МАТЕРИАЛОВ

Основными характеристиками полупроводниковых материалов - с точки зрения пригодности их для создания датчиков Холла являются: удельное сопротивление или удельная проводимость и коэффициент Хо.дла (подвижность определяется этими двумя параметрами). Кратко рассмотрим основные методы измерения этих характеристик.

4-1. ИЗМЕРЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ

В технологии датчиков Холла, кроме среднего значения р (или сг), в ряде случаев необходимо знать распределение удельного сопротивления в пластине датчика Холла. Как сдедует из § 2-1-2-3, неоднородность образца может быть причиной возникновения явлений, мешающих работе датчика Холла. Ниже рассматриваются обычно применяемые компенсационные методы измерения р и неоднородностей распределения р, а затем фотоэлектрический метод, позволяющий очень точно определять распределение р.

Компенсационные методы. К самым популярным методам измерения удельного сопротивления относятся компенсационные двух- и четырехзондовый методы. Эти методы подробно оппсаны Волдесом [Л. 478] и Ухлиром [Л. 477]. Принципиальная схема обоих методов показана на рис. 4-1. В случае образца правильной формы используется двухзондовая схема. Через образец пропускается ток /, а между остриямц перемещающихся зондов измеряют напряженде компенсационным методом. Значение удельного сопротивления определяется формулой

p=U4fa, (4-1)