где и - напряжение, измеренное компенсатором, s - поперечное сечение образца, а - расстояние между зондами.

Двухзондовый метод достаточно хорошо служит для определения неодпороднвсти материала. Можно выполнить зонд с рассгоя-нием между остриями от 0,1 до 0,3 лгм, что позволяет получать такого же порядка разрешающую способность зонда. Во многих случаях это дает удовлетворительные результаты, но необходимо

Рис. 4-1. Схемы измерения удельного сопротивления в полупроводниках двухзондовым (о) и че-тырехзондовым (б) методами.

К - компенсатор (измерительный потенциометр); Я - полупроводник; Л - амперметр.

подчеркнуть, что изготовление такого зонда и сохранение неи,змен-ным расстояния между остриями требует большой точности как в изготовлении, так и в работе с зондом. -

Для измерений четырехзондовым методом достаточно иметь плоский срез поверхности образца. Питающий ток поступает через внешние зонды. Между виутрениими зондами измеряется падение напряжения с помощью компенсатора. Чаще всего применяется головка с четырьмя зондами, расположенными на расстоянии I ям. один от другого. Тогда для определения удельного сопротивления служит формула

„ и

= 2пд -J--

(4-2)

Головка с четырьмя зондами практически непригодна для определения неоднородностей, так как ее разрешающая способность мала, а изготовление головки с расстоянием между зондами, меньшим 1 мм, представляет очень большие трудности.

Так как формула (4-2) предназначена для измерения удельного сопротивления па полубесконечном образце, то в случае образца с не очень большими размерами необходимо вводить соответствующие поправки. Таблицу поправок для четырехзондового метода измерения удельного сопротивления разработал Ухлир [Л. 477]; поправки, чаще всего встречающиеся при измерениях на холловских. пластинах, приведены в табл. 4-1-4-3. Удельное сопротивление определяется из зависимости

P=Ph3m/CZ),

(4-3)

где ризм - измеренное значение удельного сопротивления, CD - величина поправки, определенная из таблиц.

Таблица 4-1

11оправки для-определения уДеЛьногО сопротивления в тонком образце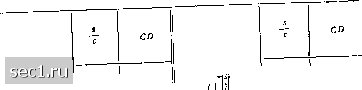

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8

,0009 ,0070 0227 ,0511 ,0939 ,1512 ,2225 ,3002

0,9 1,0 1,2 1,4 1,6 1,8 2,0 2,5

,4СС8 1,5045 1,7329 1,9809 2,2410 2,5083 2,7799 3,4674

Очень важной проблемой является наличие ряда сопутствующих протеканию тока эффектов, которые могут исказить результаты измерения удельного сопротивления. К ним относятся как контакт--ные, так и объемные явления (возникающие в случае существования неоднородностей). Влиянием контактных явлений можно пренебречь, если выполняются следующие предпосылки:

1) контакты являются невыпря.мляющими;

2) величина управляющего тока мала;

Таблица 4-2

Поправки для определения удельного сопротивления в тонком образце вблизи края

0,0 0,1 0,2 0,5 1.0 2,0 5,0 10.0

2,000 2,002 2,016 2,188 3,003 5,5 50 13,863 27,726

1,9361 1.97 1,98 2,15 2,97 5,49 13,72 27,43

1.8764

1,88

1,89

2,0i

9 87

5,34 13,32 26,71

1,5198

1,52

1,53

1,70

2,45

4,61 11,51 23.03

10,0

1,1898 1,19 1,20 1.35 1,98 3,72 9,28 13,56

1,0379 1,0Ю 1,052 1,176 1,667 3,104 7,744 15,49

1,0029 1,004 1,044 1,103 1,534 2,838 7,078 И,15Т

1,0004 1,0017 1,00И 1,0377 I ,512 2,795 6,939 13,938

Таблица 4-3

Поправки для определения удельного сопротивления

в тонком образце. Зонд установлен перпендикулярно к краю

3) расстояние 3(1нда от токового контакта больше эффективной длины диффузии носителей тока (в случае головки с двумя зондами).

Влияние объемных явлений в случае германия проанализировал Баранский (Л. 532]. К этим явлениям можно причислить:

1) неоднородность выделения джоулева тепла;

2) объемную электродвижущую силу (Баранского);

3) объемное явление Пельтье;

4) объемный эффект Томсона.

Чтобы предупредить появление указанных эффектов при измерении удельного сопротивления, необходимо, согласно Баранскому [Л. 532], ограничить плотность тока, протекающего через образец с удельным сопротивлением р»10-;-20 ом-см, значением примерно 10-15 MajcM, если градиент удельного сопротивления не превышает 50-1007o/c>t. При необходимости избежать влияния обтемной электродвижущей силы (возникающей в результате явления Бараи-,ского) хорошие результаты дает пескоструйная обработка или грубая шлифовка поверхности полупроводника. Рассмотренные эффекты особенно интенсивно проявляются в кристаллах германия и кремния, в то время как в нитерметаллических материалах в большинстве случаев они пренебрежимо малы.

Фотоэлектрический метод. Измерение фотоэлектрического напряжения, так называемого напряжения Тауца, возникающего в результате прохождения избыточных носителей через освещенное пространство с градиентом удельного сопротивления, позволяет выявлять очень малые неолнооодности распределения р. О возникнове-

„ИИ напряцеиия Тауца в УГТ Схема, служащая для Щ/ с целью опре-ческого напряжения в "°У"Р°°«"™°„с 4-2 (Л. 465]. При помощи деления неоднородности, показана на рис. ч i

Риг 4-2 Схема установки для измерения рас-„ределения удельного сопротивления фотоэлектрическим методом [Л. 465].

7 ла«па осветителя; 2 - оптическая система; 3

-Го7сто17кеГТ-!=с/то1

потенциометр).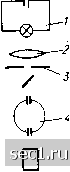

£1

соответствующей оптической системы исследуемый образец, находящийся на перемещающемся предметном столике, освещается световым лучом. Образец закрепляется двумя свинцовыми заи<имами, на которых компенсационным методом измеряется значение фотоэлектрического напряжения. Измерение неоднородности основано на построении карты значений фотоэлектрического напряжения, которое пропорционально значению градиента удельного сопротивления.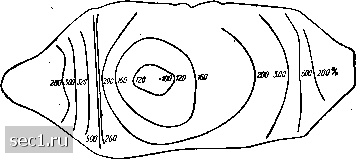

Рис. 4-3. Пример картины Распределения удетьиого со р

в кристалле германия. Величина р=0,46 ом-см ъ точке luu v

за 100%. 79

Измеряя возможно точнее удельное сопротивление в одной точке образца двух- или четырехзондовым методом, можно затем пересчитать по распределению фотоэлектрического напряжения распределение удельного сопротивления, принимая измеренное значение р за условный уровень.

На рис. 4-3 показано распределение удельного сопротивлеиич в кристалле германия. Необходимо, однако, отметить, что этот кристалл имеет заранее предусмотренные большие значения градиента удельного сопротивления. В обычных кристаллах германия, полученных методом Чохральского, значение grad р колеблется в пределах 5-30%1см. Этот метод использовался уже для исследования неоднородностей в кристаллических образцах германия, кремния н антимоннда индия [Л. 465].

4-2. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА ХОЛЛА

Коэффициент Холла определяют по измерениям напряжения Холла в соответствии с формулой (2-436). Как известно из предыдущих разделов, явлению Холла сопутствует ряд других эффектов, которые могут существенным образом влиять на значение измеряемого напряжения. В случае измерения на постоянном токе выходное напряжение будет представляться следующей суммой:

= V + "уВ + yNB + lyRL + + UyT + y, (4-4)

где UyH - напряжение Холла; UyE - напряжение Эттингсгаузена, f-yNE - напряжение Нернста-Эттингсгаузена, Ууш. - напряжение Риги-Ледюка, (Уо - линейное резистивное остаточное напряжение, (Уут - термоэлектрическое напряжение, СУу» - иапряженне Тауца, возникающее из-за инжекции носителей.

В большинстве случаев напряжением Uyw можно пренебречь по причинам, изложенным в § 5-6. Выполняя измерения прн поочередно 113Л1епяющнхся направлениях 1х и В, получаем следующую систему уравнений {Л. 295]:

и, (/, В) = + -f Uyfs + UyRt + fs. + Uyv - (- /, B) = - - U -b f/H+fRL- Uyry ( /. B) = f/ + U, - U,, - U, - f/,. -f U,;

Из вышеуказанных уравнений получается следующее ьыраже-

(4-5)

+ JyB----•

(4-6)

Как следует нз формулы (4-6), выполняя поочередно четыре и:чмерения напряжения Холла, можно исключить четыре паоазитиых напряжения; только напряжение Эттингсгаузена неотдели.чо от напряжения Холла. Однако необходимо подчеркнуть, что это справедливо только в случае, когда напряжения Нернста-Эттингсгаузена и Риги-Ледюка возникают в результате теплового потока, вызван-

ного неоднородностью образца, а не теплом Пельтье, поток которого изменяет свое направление прн смене полярности тока Ix-В таком случае напряжения Нернста-Эттингсгаузена и Риги- Ледюка не удалось бы исключить.

Многократное измерение напряжения Холла дает достаточно хорошие результаты, но является очень трудоемким. Эти "измерения значительно облегчаются при использовании пере.менных тока или индукции. В случае измерений на переменном токе могут иметь место следующие варианты:

1. Управляющий ток является переменным /j:=/.cm sin о)/, а ин-дункция B = const или наоборот В = Вт sin (о, а /i = const.

2. Ток 1х и магнитная индукция В - переменные (/i= =1хт sin at, а также В = Вт sin mt).

3. Ток Ix и магнитная индукция В - переменные, но имеют разные частоты: Ix = Ixmsmii)it; В = Вт sin (Ozt.

Напряжение Холла UyH, а также напряжение Эттингсгаузена UyE зависят как от тока, так и от индукции. Сопутствующие остаточные напряжения Uyo, Uyr и Uyw являются функциями 1х, а UyNE и UyRL, а также напряжение, индуктируемое в проводниках, UyB - являются при определенных значениях тока 1х функциями магнитной тцукции (§ 5-6).

В т;л),ч. 1-4 собраны дашшю относительно характера отдельных напряжепий, сопутствуюи;их напряжению Холла при разных условиях его измерения. [Гапряжеиия термоэлектрического характера, т. е. сооствешю термоэлектрические 11;нрнжеине, а также напряжения, возникающие вследствие явлений Эттингсгаузена, Нернста - Эттингсгаузена и Риги-Ледюка, имеют сомиож;-1тсль &~°1"о (где (Оо - бeзpa;мepиaя постоянная), описывающий умспьпгение эгих напряжепий но мере роста частоты напряжения питания. Это объясняется тепловой инерцией этих явлений. В табл. 4-4 обрамлением клеток отмечены напряжения, которые возникают вместе с напряжением Холла во время пзмерепня, т. е. имеют ту же самую частоту. Напряжения в необрамлсниых клетках в дашюм измерении исключаются. Из таблицы видны преимущества, которые достигаются благо.чаря ирименеиию для измерения напряжения Холла пе-. ременного питающего напряжения.

1, В случае питания образца переменным током при постоянной магнитной индукции {К« 1 в табл. 4-4) исключаются напряжения UyNE, UyRL, а прн использовании достаточно высокой частоты питающего тока устраняются также напряжения .UyE и UyT- Поэтому при осуществлении указанных условий получаем следующее выражение для выходного напряжсння;

Uy = U„ + Uy, + U

(4-7)

2. В случае переменного магнитнсго поля, при достаточно большой частоте й при постоянном питающем токе (№ 2 в табл. 4-4),

получается

Uy:=UyH.+ UyB+"yB-

.(4-8)

3. В случае, когда оба управляющих сигнала переменные н одной частоты, получаем иа второй гармонике:

Uy = Uf,+Uyr

6-140)

(4-9)