отличается кремниевый датчик Холла с удельным сопротивлением 10 ом-см; дальше «дут датчики Холла из германия, а затем с небольшими уже отличиями датчики Холла из InAso,8Po,2, InSb, InAso,6Po,4 и InAs. В случае пленочных датчиков Холла лучшими свойствами отличается датчик Холла, изгото;вленный из InSb, выходное напряжение которого в 15-30 раз больше выходного напряжения других пленочных датчиков Холла и в 2-20 раз больше напряжения кристаллических датчиков Холла.

Таблица 5-2

Максимальное выходное напряжение и вольтовая (магнитная) чувствительность датчиков Холла с размерами а=1,2 см, 6=0,6 см и толщиной с (v=0,004 вт град и В=1 кгс)

Материал

fp=0,5 ом-см 1р=1,0 ом-см

р=0,5 ом-см р=10 ом-см

"ь «:°з:

InAs

InAs„ „Р„ , InAs, HgTe HgSe InSb CdjAsj

CM-" WcM-

O.sP 0,2

0,01 0,01

0,01 0,01

0,01

0,01

0,01

0,0!

0,0! !,3.!0-* 4,2.lO-* 2.10-* 2.10-*

CMI к

дг, °C

(OM-CM)-

3 000

4 200

550;

2G000

80 300 100 !80 250 13 Ю,7 400 9,3

70 40

300 150

50 10 80 250 200 80 100 25 80

2 0,1

уЯмакс

мквгс

0,191

0,144

0,084 0,54

0,080 0,051 0,067 0,084 0,103 0,077 0,055

0,038

191 144

84 540

80 51 67 84 103 77 55 1 100 38

Следующим из основных параметров датчика Холла является его чувствительность. Существуют два определения чувствительности, -причем первое из них связано с максимальным выходным напряжением и определяется

(5-13)

В последней колонке табл.5-2 дано значение v которое пропорционально значению [/.я.макс В отличие от другого определения чувствительности, данного ниже - чувствительность у будем называть вольтовой (магнитной) чувствительности,

Второе определение рассматривает чyвcтвитeльoctЬ датчика Холла как напряжение Холла, полученное при единичном управляющем токе и единичной магнитной индукции, и согласно зависимости (2-436) выражается формулой -

Выражается она обычно в в/а-кгс. Чувствительность, определенная согласно выражению (5-14), однозначно определяет накуэн статических характеристик Uy = =f{I,B). Опираясь на данные гл. 3 и 5, можно рас- / считать чувствительность у, которая может быть достиг- нута в датчиках Холла, выполненных из разных материалов при тех же предпосылках, которые использова- лись при составлении табл. 5-2. Рассчитанные величины представлены в табл. 5-3.

Таблица 5-3

Чувствительность датчиков Холла

Среди кристаллических датчиков Холла наибольшую чувствительность имеют датчики Холла, изготовленные из материалов с большим коэффициентом Холла - кремния и германия; наименьшую чувствительность имеют датчики из InAs. Пленочные датчики Холла в среднем отличаются большей чувствительностью, чем кристаллические. При этом необходимо подчеркнуть, что если технология кристаллических датчиков уже отработана, то технология напыленных датчиков Холла еще продолжает изучаться.

а) б)

Рис. 5-1. Распределение эквипотенциальных линий в полупроводниковой пластине.

а - удельные сопротивления контактов и пластины одинаковы; б - удельное сопротивление контакта значительно меньше, чем пластины.

5-3. ШУНТИРУЮЩЕЕ ДЕЙСТВИЕ УПРАВЛЯЮЩИХ KOHtAKTOe

В формуле (2-436), по которой определяется напряжение Холла, имеется только один размер пластины, а именно ее толщина. Эта формула справедлива, однако, только в случае бесконечно длинной пластины с точечными электродами Холла. На практике проявляется зависимость напряжения Холла от длины и ширины

пластины. Это происходит вследствие того, что часть напряжения Холла замыкается накоротко через электроды, выполненные из материала с гораздо меньшим удельным сопротивлением, нежели удельное сопротивление полупроводника. Визуально это можно представить так, как показано на рис. 5-1. Он представляет (рис. 5-1,а) распределение эквипотенциальных линий в магнитном поле в случае, когда ток 1х подводится ко всей ширине пластины с помощью электродов с такими же электрическими свойствами, что и полупроводник. Рисунок 5-1,6 соответствует случаю, когда удельное сопротивлеиие электродов «амного меньше удельного сопротивления полупроводника. Этот факт вызывает деформацию эквипотенциальных линий. На величину этой деформации влияет также ширина холловских электродов. В связи с этим формула для выходного напряжения в датчике Холла приобретает следующий вид:

= (5-15)

где S - ширина холловоких электродов. Он -поправочная функция.

Определением поправочных функций занимались многие авторы [R. 131, 213, 298, 502]; это, однако, связано с рядом расчетных трудностей. Липман и Курт определили поправочную функцию для пластины в форме прямоугольного параллелепипеда с точечными хол-ловскими электродами [Л. 298]. Полученный результат показан на рис. 5-2. Поправочную функцию, учитываю-

щую влияние ширины холловских контактов, для конкретного материала (InAs) с коэффициентом Холла /?н = 100 CMJK в зависимости от величины поля вычислили Курт и Хартель [Л. 280] (рис. 5-3). Однако трудности расчета ие позволили получить универсальных данных, таких ка.к для случая шунтирующего действия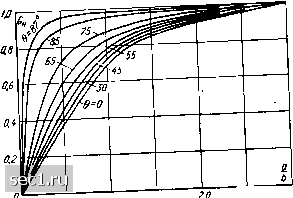

0,5 .и

Рис 5-2. Зависимость поправочной функции G отношения о/Ь и угла в [Л. 298].

2,5 5,0 1я от

,.гчпппв Гпис 5-2) О влиянии ширины по-Х™л\ГыГК;р1;в- харакхер„с™к„ датчика

П"рХ;еТл. ?24%р-ведена поправочная функция

,l.„«.nnnHnro магнитного поля, а Уик

Рис. 5-3. Ход поправочной функции J-om влияниярины холловских электродов в материале с /?я -100 сл /к \п. zouj

[Л. 502] рассчитал поправочную функцию для полупроводниковых пластин разной формы (например, круглых, шестиугольных и т. п.), которые могут найти применение в невзаимных элементах на основе датчиков Холла

(см. § 19-7). Разработан также ряд математических аналоговых методов, позволяющих определить поправочную функцию при разных конфигурациях пластины датчика [Л. 57, 99, 187, 330].

•Липман и Курт [Л. 297] определили также зависимость эффекта магнитосопротивления от формы электродов. Они отметили, что относительный рост сопротивления в магнитном поле можно описать следующей функцией:

дующем виде: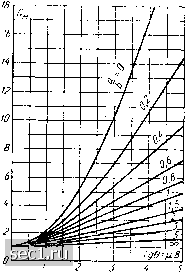

(5-16)

Рис. 5-4. Зависимость поправочной функции См от отношения а/6 и угла 9 (Л. 297],

где рв/ро-прирост удельного сопротивления <в бесконечно длинном образце (физический эффект магнитосопротивления), в - угол Холла.

Результаты расчета Липмана и Курта [Л. 297], представ-ляющие зависимость

рис. 5-4.

м = ~rT~ - f (S показаны на

5-4. НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИК ДАТЧИКОВ ХОЛЛА, СВЯЗАННЫЕ С ГЕОМЕТРИЕЙ, ЭФФЕКТОМ МАГНИТОСОПРОТИВЛЕНИЯ И СОГЛАСОВАНИЕМ НАГРУЗКИ

Как показано в предыдущем параграфе, в датчике Холла имеет место зависимость сопротивления и чувствительности от геометрических размеров, а также от индукции. Эти зависимости мол<но представить в сле-92

Х.УО ро \

, В у,

(5-17) (5-18)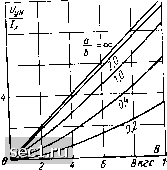

где Rb, Рв - сопротивление пластины и удельное сопротивление полупроводника в магнитном поле В, 7?о,ро-сопротивление пластины ;И удельное сопротивление полупроводника в отсутствие магнитного поля, Ом, Gh - поправочные функции для эф- ,0 -----"

фекта магнитосопротивления ff/a и явления Холла соответ- gg ственно.

Результатом существова-ния зависимостей, описываемых формулами (5-17) и (5-18), является нелинейность характеристик датчика Холла относительно магнитной индукции. На рис. 5-5 показаны характеристики датчиков Холла, изготовленных на основе арсенида индия, с различными значениями а/Ь (т. е. отношения длины к ширине) [Л. 183, 184]. Лучшая линейность статических характеристик получается при a/b>3. Величина этого отношения существенно влияет также на зависимость сопротивления пластины датчика Холла от индукции В. На рис, 5-6 приведены соответствующие характеристики датчика Холла из антимонида индия [Л. 183, 184]. Как можно заметить, и в этом случае выгоднее использовать пластины с большой величиной ajb, так как при этом получается малая зависимость активного сопротив-

Ркс. 5-5. Экспериментальные характеристики датчшюв Холла ««, = f(B. - [Л. 183].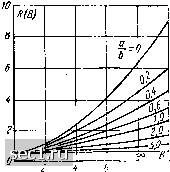

8 кгс Ю

Рис. 5-6. Экспериментальные зависимости магнитосопротивления от формы пластины в датчиках Холла из InSb [Л. 183].