щей книги. Далее это на1;*яжение будет обозначаться UyH- В принятой системе координат составляющая U - = 0. Однако в случае, когда угол между i и В не является прямым, появляется и составляющая U, называемая планариым эффектом Холла [Л. 153]. Этот эффек описывается формулой (2-44)

(2-44)

где aj) - угол между i и В.

Рассмотрим теперь некоторые вопросы, связанные с выяснением смысла коэффициента Холла Ян- Из уравнений (2-42) и (2-43) можно получить зависимость, из которой вытекает физический смысл Rh-

(2-45)

Как следует из этого выражения, коэффициент Холла однозначно определяется концентрацией носителей тока в полупроводнике. Эта формула одновременно показывает большую важность измерений коэффициента Холла для исследования физических свойств полупроводника.

Приведенные выше рассуждения, относящиеся к полупроводнику п-типа, можно выполнить совершенно аналогично и в случае полупроводника р-типа. В этом случае коэффициент Холла будет выоажаться зависимостью

(2-46)

где р -концентрация дырок.

В случае полупроводника со смешанной проводимостью, т. е. в том случае, когда величины пр„ и рхр сравнимы (что может иметь место в собственных полупроводниках), выражение для коэффициента Холла принимает более сложный вид:

(2-47)

Рис. 2-11. Зависимость коэффициента А от отношения p.i/p [Л. 530].

Осталось рассмотреть еще влияние механизма рассеяния носителей тока на коэффициент Холла. На самом деле в уравнения (2-45) - (2-47) следует ввести еще коэффициент А, величина которого зависит от механизма рассеяния носителей тока в кристаллической решетке, так что, например, зависимость (2-45) примет вид:

Янп = -АЫе. (2-48)

В случаях, когда определяющим является рассеяние на нейтральных атомах примеси или когда полупроводник вырожден (очень большая концентрация примеси), коэффициент Л=1; в случае рассеяния на тепловых колебаниях решетки Л = Зя/8= = 1,18; в случае рассеяния на

ионизированных примесях /1 = 1,93. На рис. 2-11 [Л. 530] показана зависимость коэффициента А от отношения сопротивлений pj/p; здесь р -удельное сопротивление, соответствующее рассеянию на ионах чужеродных атомов, а р - полное удельное сопротивление.

2-5. ЭФФЕКТ МАГНИТОСОПРОТИВЛЕНИЯ

Под названием «эффект магнитосопротивления» (или эффект Гаусса) подразумевают наличие зависимости удельного сопротивления полупроводника от магнитного поля. Это явление вызвано тем, что носители тока, перемещающиеся в полупроводнике под действием электрического поля, не имеют одинаковых скоростей, как предполагалось в § 2-4. Скорости носителей тока различны и подчиняются распределению, отвечающему статистике Ферми - Дирака. В результате этого поперечное поле Холла компенсирует влияние силы Лоренца только на носител-и тока, имеющие среднюю скорость v. Поэтому будут существовать носители тока (со скоростью, большей или меньшей у), траектория которых будет искривлена, что приведет к увеличению числа столкновений (сокращение длины свободного пробега) и тем самым - к повышению удельного сопротивления полупроводника. 3* 35

Согласно Вайсу и Велькеру [Л. 495] приращение удельного сопротивления в полупроводнике для случая слабых магнитных полей (т. е. при условии цВ<1) описывается формулой

fi = = ~ (-) (пВу. (2-49)

В случае участия в проводимости носителей тока обоих знаков эта зависимость будет описываться несколько другим уравнением

4 Р-1п + >1р

(2-50)

Наивысшую возможную величину Ар/рв в данном полупроводнике можно найти (зная зависимости fx„ и iip от концентрации) из следующего выражения:

(2-51)

где 6 = (x„/iip.

Из этих формул следует, что приращение сопротивления в области малыхмагнитных полей пропорционально квадратам подвижности и магнитной индукции. Очень удобную формулу, приближенно описывающую эффект магнитосопротивления в большом диапазоне значений индукции, предложил Хардинг [Л. 179]:

1 -f •

(2-52)

где Л- постоянная. Из (2-52) следует, что при малых В величина Ар/ро квадратично зависит от В, тогда как при больших В Ар/ро достигает насыщения (что подтверждается и на опыте).

Очень часто для описания эффекта магнитосопротивления применяют также приближенную формулу

ГДр

(2-53)

где а и п 36

постоянные.

Явление магнитосопротиления зависит также от формы образца, поскольку поле Холла зависит от его размеров (см. § 5-3).

2-6. НЕКОТОРЫЕ ОСОБЫЕ СЛУЧАИ ПРОЯВЛЕНИЯ ЭФФЕКТА ХОЛЛА

1-4-1. вторичный эффект холла

Под вторичным эффектом Холла понимают появление на токовых электродах напряжения Холла, вызванного протеканием тока между потенциальными электродами. Поэтому вторичное напряжение Холла будет подчиняться зависимости

(2-54)

Напряжение U„x складывается с напряжением питания датчика Холла Ux=Rxfx, вследствие чего действительный управляющий ток датчика Холла будет зависеть от магнитного поля не только благодаря эффекту Гаусса, но и благодаря вторичному эффекту Холла. Рассмотренный эффект является также одной из причин нарушения линейности характеристики датчика Холла.

г-6-г. собственный эффект холла (я. 2141

Протекание тока в проводнике Рис. 2-12. Распре-СОпрОВОЖДаетСЯ возникновением деление напряжен-

магнитного поля. Поэтому и ток, «-™ eo"!" протекающий через датчик Холла, молинейного про-создает магнитное поле, которое мо- водника с током, жет быть причиной возникновения эффекта Холла. Однако, как следует из теории магнитного поля, в случае проводника с круглым сечением магнитное ноле имеет только тангенциальную составляющую (в соответствии с рис. 2-12), равную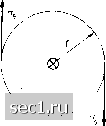

Я„ = 21гг,

(2-55)

где / - ток, протекающий через проводник, г-расстояние от проводника.

Рассматривая в соответствии с изложенным обычную холловскую пластину, можно показать, что в случае точной геометрической симметрии значения напряжения

Холла, возникающих в обеих половинах пластины (относительно оон симметрии, параллельной направлению тока), будут прямо противоположны и скомпенсируют-ся. Отсюда следует, что собственный эффект Холла будет возникать только в тех пластинах, в которых холловские электроды расположены несимметрично относительно оси X.

2-«-3. фотоэффект холла

Освещение поверхности полупроводника приводит к образованию в нем пар носителей тока дырка -электрон, т. е. к инжекции носителей тока. Освещенный полупроводник, находящийся в магнитном поле, даст при измерениях другую величину коэффициента Холла, нежели неосвещенный полупроводник. Это явление называется фотоэффектом Холла.

Изучением этого эффекта в полупроводниках занимались Мэсон [Л. 314] и Добровольский [Л. 580]. Последний показал, что освещение полупроводника всегда приводит к уменьщению напряжения Холла, а величина этого уменьшения пропорциональна прежде всего концентрации инжектированных носителей тока, а также углу Холла и подвижности носителей.

2-7. ДРУГИЕ ГАЛЬВАНО. И ТЕРМОМАГНИТНЫЕ ЯВЛЕНИЯ

Рассматриваемые в этом параграфе гальваномагнитные (кроме эффектов Холла и Гаусса) и термомаглит ные явления сопровождают основное явление в датчиках Холла -эффект Холла. Проявление этих эффектов может исказить характеристики датчика Холла.

Гальваномагнитные эффекты возникают под воздействием поперечного магнитнаго поля при протекании" через образец электрического тока. В то же время для термомагнитных эффектов первичными являются тепловой поток и нормальное к нему магнитное поле. Рассматриваемые эффекты Стильбанс классифицировал в виде следующей таблицы Л. 668] (см. табл. 2-1).

Причиной возникновения остальных гальвано- п гер-момагнитных эффектов является распределение по скоростям носителей тока, принимающих участие в проводимости. Поле Холла в стационарном состоянии долл-сно иметь такую величину ,чтобы тока в направлении оси у не появлялось. Результирующая сила, действующая на

Таблица 2-1 Классификация гальвано- и термомагнитных эффектов

носители тока в этом направлении, будет равна нулю только для носителей тока со средней величиной энергии, тогда как носители с энергией, отличающейся от средней, будут стремиться к боковым граням пластины, вызывая появление добавочных как электрических, так и термомагнитных эффектов.

Легко заметить, что из приведенных в табл. 2-1 гальвано- и термомагнитных эффектов существенную роль будут играть только поперечные эффекты, поскольку величина продольных эффектов пренебрежимо мала по сравнению с напряжением питания. Ниже приведены определения и краткие характеристики отдельных поперечных эффектов.

Эффект Эттингсгаузена заключается в появлении поперечной разности температур под влиянием протекающего через образец тока и перпендикулярного к нему магнитного поля. Величина температурного градиента определяется зависимостью

где Р -коэффициент Эттингсгаузена.

(2-56)