ПОВЕРХНОСТНЫЕ ВОЛНЫ

г. ASEBCTPOnOB

Электромагнитные волны в свободном пространстве распространяются со скоростью, равной скорости света.

Если предположить, что пространство заполнено диэлектриком с диэлектрической проницаемостью е, большей диэлектрической проницаемости свободного пространства во, то скорость волны уменьшилась бы в уе/ед раз. Волны, распространяющиеся со скоростью, меньшей скорости света, обычно называют медленными. Медленные волны могут, например, распространяться между двумя бесконечными идеально проводящими плоскостями или в коаксиальной линии, если пространство между проводниками заполнить диэлектриком. В этих случаях волна замедляется также в У г/е раз. Обычно медленные волны характеризуют замедлением т, которое определяется

где V - фазовая скорость медленной волны, k - постоянная распространения волны в свободном пространстве, ki - постоянная распространения медленной волны.

с1тличительной особенностью медленных волн является то, что они могут направляться однопроводными линиями, локализуясь у границы раздела однопроводной линии со свободным пространством. Медленные юлны, направляемые однопроводными линиями, называются поверхностными волнами. Можно показать, что если волна распространяется вдоль регулярной границы раздела дух сред (например, границы раздела сюбодного пространства и однопроводной линии) со скоростью, меньшей с, то энергия, переносимая волной в верхнем полупространстве, локализуется у границы раздела: амплитуда поля экспоненциально убывает при удалении от границы раздела.

Поверхностные волны впервые были обнаружены Ценнеком в 1907 г. при решении задачи о распространении радиоволн вдоль проводящей плоской поверхности земли. Поверхностная волна Ценнека не играет существенной роли при распространении радиоволн. Это объясняется главным образом неэффективным ее возбуждением. Однако, если принять специальные меры, то принципиально можно достигнуть почти полного перехода энергии излучателя в энергию поверхностной волны. Наиболее просто поверхностные волны могут быть возбуждены в диапазоне СВЧ, например, над цилиндрическим проводником с конечной проводимостью. Это дает возможность практического применения поверхностных волн в линиях передачи электромагнитной энергии, в антенной и волноводной технике, в линейных ускорителях частиц, в генераторах и усилителях диапазона сверхвысоких частот.

В настоящее время существует большое число работ, посвященных теории и практическому применению поверхностных волн. Мы изучим основные свойства поверхностных волн на конкретном примере и обобщим полученные результаты на другие случаи.

1. Поверхностные волны, направляемые диэлектриком

Поверхностные электромагнитные волны могут распространяться над системами, изображенными на рис. 1. Основной частью этих систем является диэлектрический слой, находящийся в свободном пространстве или нанесенный на металлическую поверхность. Для простоты рассмотрим сначала простейшую из этих систем (рис. 1, а), представляющую собой бесконечный диэлектрический слой, лежащий на плоскости с идеальной проводимостью. Будем считать, что поля не зависят от координаты z.

Задача определения полей в такой системе сводится к отысканию решения уравнений Максвелла.

rotH = швЕ,

rotE=-шцН, (2)

(где Е и Н - векторы напряженности электрического и магнитного полей, вир,- электрическая и магнитная проницаемости среды, t*= -I; зависимость во времени взята в форме е"), удовлетюряю-щих условию равенства нулю касательных составляющих поля у металлической пластины и непрерывности касательных составляющих полей Е и Н на границе раздела диэлектрика и сюбодного пространства.

: В системе диэлектрическая пластина на металле могут распространяться электрические (типа Е) и магнитные (типа И) волны, характеризующиеся тем, что в первом случае составляющая Ех ф

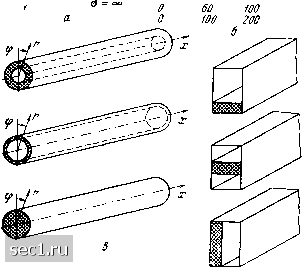150 Ex 300 Ey

Рис. 1. Диэлектрические системы с поверхностными волнами

а - диэлектрический слой на бесконечной плоскости с идеальной проводимостью; б - структура полей; в - цилиндрические системы; г - волновод, частично заполненный диэлектриком

=f= О, а Нх= О, во втором случае Я =f= О, а £=0. Причем ось х совпадает с направлением распространения волны.

Для конкретности рассмотрим решение задачи для волны типа Е. Все составляющие полей в соответствии с уравнениями (2) в этом случае могут быть выражены через магнитный вектор Hz

шг ду

где составляющая поля Нг удовлетворяет двумерному уравнению Гельмгольца

Предполагая, что в направлении распространения поля изменяются по закону g-*, получим решение для верхнего полупространства

Н, = Ное- е - ,

Еу = Норуе - 1= е -

£, = ЯорУ1-г (5)

где р = - волновое сопротивление свободного пространства.

Физическим условиям удовлетворяет ветвь корня

тУТ*<0. (6)

Формулы (5) показывают, что поле локализуется у гранищл раздела при у > 1 (медленные волны). При у < 1 решение (5) дает плоскую волну, распространяющуюся под углом а (cosa = у) к границе раздела.

Для определения у необходимо найти поля в среде 2. Это решение имеет вид

Яг = Япсоз

ka{y + a) -1

Еу = ЯоР cos [ka {у + а) \/ -у]е-, (7)

Ех = /Яор - sin [ka(у + а) - г] е-*.

Приравнивая касательные составляющие полей решений (5) и (7) при у = О и деля одно из получившихся уравнений на другое, находим уравнение для определения у

где введено обозначение

Величина Zn, равная отношению касательных составляющих электрического и магнитного полей, определенных в среде 2, на границе раздела сред носит название поверхностного импеданса.

Так как решение в среде 3 мы искали независимо от среды 2, то из уравнения (8) и условия (7) следует, что поверхностная волна

типа Е может существовать при индуктивном поверхностном импедансе. Если аналогичное решение проделать для волны типа Н, то получим, что поверхностная волна окажется возможной только при емкостном поверхностном импедансе.

Здесь следует заметить, что в ряде случаев поверхностный импеданс можно считать независимым от поля во внешней среде, поэтому он часто рассматривается как граничное условие на границе раздела двух сред и широко используется в теории поверхностных волн.

Возвращаясь к нашему конкретному случаю, преобразуем уравнение (8) к виду

Из этого уравнения следует, что с ростом толщины диэлектрика ka замедление y стремится к значению Уе/ец, следовательно, концентрация поля в диэлектрике увеличивается. Аналогичное явление происходит с ростом е. При больших значениях е (е >• 10) можно получить резкую зависимость замедления от толщины диэлектрика и длины волны.

Поверхностные волны типа Е принципиально могут распространяться при сколь угодно малой толщине диэлектрика. Это не относится к поверхностным волнам типа Н, которые могут распространяться только начиная с определенной толщины диэлектрика при заданном значении е, так как импеданс в этом случае должен быть емкостным.

Графики распределения полей для волны типа Е приведены на рис. 1, б.

Поверхностная волна, совпадающая по структуре с рассмотренной, может распространяться в диэлектрике без металла. При этом все полученные формулы сохраняются, если толщину диэлектрической пластины взять удвоенной по сравнению с диэлектрическим слоем. Эго очевидно, если воспользоваться принципом зеркального отображения. Получающийся тип волны, направляемой пластиной, называется четным, так как вертикальные составляющие напряженности электрического и магнитного полей сверху и снизу от пластины совпадают по направлению. Пластина может также направлять и нечетные типы волн, когда вертикальные компоненты полей сверху и снизу от пластиНы отличаются знаком.- ;

Поверхностные волны, аналогичные рассмотренным, могут распространяться над цилиндрическими поверхностями (рис. I) в), а также в волноводах, частично заполненных диэлектриком (рис. 1,г)

Распространение поверхностных волн над диэлектриком тесцо связано с явлением полного внутреннего отражения при падении плоской волны из диэлектрика на плоскую границу раздела с менее

оптически плотной средой. Если в (7) представить косинус и синус через экспоненциальную функцию, то эти формулы мы можем трактовать как сумму двух плоских волн, распространяющихся под углом друг к другу, отражаясь от границы раздела диэлектрика со свободным пространством и металла с диэлектриком. Из-за того, что угол падения на границу раздела больше угла полного внутреннего отражения, плоские волны не проходят в среду 3, а лишь индуцируют в нем поля, экспоненциально убывающие от поверхности.

2. Поверхностные волиы, направляемые

искусственными замедляющими структурами

Индуктивный или емкостной поверхностный импеданс может быть создан не только с помощью диэлектрика, но и искусственным образом с помощью различных прорезей или выступов, сделанных

]Штпт1шлтш ruuimnuuup"" .: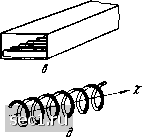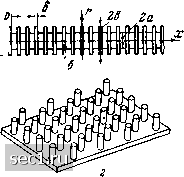

Рис. 2. Системы поверхностных волн с искусственными замедляющими структурами

а - плоская ребристая поверхность; б - ребристый стержень; в - ребристый волновод; г - штырьковая замедляющая структура; д - цилиндрическая спираль

В металлической плите. Различные типы искусственных замедляю щих поверхностей, применяемые в антенной технике, приведены на рис. 2.

Простейшим и наиболее широко распространенным типом таких поверхностей является ребристая поверхность (рис. 2, а). Так как ребристая поверхность имеет периодичность вдоль направления распространения, то граничные условия не могут быть удовлетворены только одной пространственной гармоникой в области 3,