а только бесконечной суммой пространственных гармоник:

£л: = 2 С"„ ехр

п = - оо

Т + п-

хехр[-г>/"1 (г + л-

(10)

где Сп - амплитуды пространственных гармоник, р - период ребристой структуры.

Однако, если период структуры мал по сравнению с длиной волны (-~- > lOJ, то нулевая гармоника достаточно точно описывает поле в верхнем полупространстве. Поле в канавках также может быть описано только основной ТЕМ волной Тогда входное сопротивление канавки

2BX = 2ptgM,

а усредненный поверхностный импеданс

Zn = /otptgM, (И)

где а = ; б - толщина ребра; h - глубина канавки.

Поле в полупространстве в этом случае описывается формулами (5), а дисперсионное уравнение (8) преобразуется к простому виду

Y=yi -f aMgM. (12)

Из этой формулы следует, что, увеличивая глубину канавки, можно получить сколь угодно большое замедление поверхностной волны. Однако это несправедливо, так как формула (12) приближенна. Практически длина поверхностной волны не может быть короче удвоенного периода структуры. При возрастании замедления поверхностной волны растет его зависимость от частоты. Это обстоятельство находит практическое применение в антеннах с качанием луча. Рост замедления приводит к концентрации электромагнитного поля у поверхности металла и, таким образом, к росту омических потерь и уменьшению пропускаемой мощности.

Потери энергии могут быть рассчитаны, если воспользоваться полями в канавках, найденными при идеальной проводимости металла. При известной напряженности магнитного поля плотность токов, наведенных на поверхности, J = [пН], следовательно, мощность, теряемая на тепло на единице поверхности, Рпот = \J\ rs (fs - поверхностное сопротивление металла).

Затухание электромагнитной волны в децибеллах на метр определится из выражения

гр

(13)

где Рпот - мощность, теряемая волной при прохождении единицы длины; Р - мощность, переносимая поверхностной волной.

Расчеты и эксперимент показывают, что в трехсантиметровом диапазоне волн при замедлении у = 2,5 потери равны 3-5 дб/м в зависимости от шага структуры, достигают 8-10 дб/м при замедлении Y = 3 и уменьшаются до 2-3 дб/м при замедлении Т = 2.

При неизменном замедлении потери обратно пропорциональны длине волны в степени /г. Исследования показывают, что заполнение канавок диэлектриком при том же замедлении приводит к увеличению потерь.

Ребристые замедляющие поверхности получили применение в антеннах с электрическим качанием луча путем изменения частоты. В этом случае требуется, чтобы при максимальной крутизне замедления, как функции частоты, омические потери были минимальными. С этой точки зрения представляет интерес сравнить ребристые поверхности с диэлектрическим слоем, лежащем на металле. Расчеты показывают преимущество ребристых структур перед диэлектрической системой, так как потери в последней больше, если даже предположить тангенс угла потерь диэлектрика равным нулю, а диэлектрик расположить на пластине из серебра.

Важное значение при применении ребристых поверхностей имеет величина пропускаемой ребристой поверхностью мощности, которая определяется максимально допустимой величиной напряженности электрического поля. Поля Ех и Еу сдвинуты на л/2 по фазе, и поэтому величина пропускаемой мощности определяется максимальной из них. Если учитывать только нулевую гармонику поверхностной волны, то можно показать, что (£y>£:. Мощность, пропускаемая поверхностью шириной D, может быть найдена из (5)

(14)

где £пред - предельно допустимая напряженность поля составляющей Еу нулевой гармоники. Известно, что для воздуха £пред = = 3 кв/мм. Однако из-за пространственных гармоник суммарная составляющая поля Еу существенно возрастает (концентрация поля у острых краев ребер), что уменьшает примерно в 2 раза предельно допустимую напряженность поля нулевой гармоники. Концентрация поля может быть уменьшена при закруглении ребер структуры (примерно на 30% при радиусе закругления, равном половине толщины ребра). Расчеты и эксперимент показывают, что ребристая структура с закругленными ребрами шириной, равной длине волны, может пропустить мощность 35 кет при v = 2,5 в трехсантиметровом диапазоне волн.

Аналогично случаю диэлектрического слоя с металлической подложкой поверхностные волны могут распространяться над цилиндрической и другими типами ребристых поверхностей. Особый интерес представляют симметричные и несимметричные типы волн, распространяющиеся вдоль ребристого стержня (рис. 2, б). Поля в этом случае во внешнем пространстве и в канавках описываются с помощью цилиндрических функций целых индексов.

Ребристая структура может быть использована для замедления электромагнитных волн в прямоугольном волноводе (рис. 2, в). Для этого дно волновода должно быть выполнено в виде ребристой структуры конечной ширины. Локализация поля у импедансной

поверхности наблюдается при Y > Р, где Р= 1 A.j за.

медление в волноводе без канавок.

Ребристые волноводы наряду с открытыми ребристыми поверхностями находят применение в антенной и волноводной технике.

Система цилиндрических штырей, установленных на металлической поверхности (рис. 2, г), создает индуктивный поверхностный импеданс и, таким образом, может направлять поверхностную волну. При малом диаметре штырей и расстоянии между ними штырьковая замедляющая система обладает анизотропными свойствами по отношению к направлению распространения волны над границей раздела. Это достоинство системы используется при создании антенн поверхностных волн.

Особый класс замедляющих систем составляют системы, которые могут быть названы геометрическими. Типичным представителем этих систем является однозаходная цилиндрическая спираль (рис. 2, д).

Электрический ток в спирали может быть представлен в виде суммы пространственных гармоник. В зависимости от геометрических характеристик спирали и длины волны амплитуда одной из гармоник может оказаться преобладающей. Это явление называют пространственным резонансом. Первый пространственный резонанс соответствует случаю, когда части витков, лежащие на одной образующей, оказываются в фазе. В антенной технике обычно используются спирали с первым пространственным резонансом.

Геометрические типы замедляющих систем позволяют получить большие замедления (10-100) и используются в различных электронных приборах СВЧ.

3. Возбуждение поверхностных волн

Возбуждение линии поверхностных волн возможно источниками, расположенными в поперечном сечении, или вдоль линии.

В первом случае для эффективного возбуждения поля источники должны воспроизводить структуру поля поверхностной волны. Если замедление волны близко к едшшце, то иоле слабо убывает при удале-

НИИ от импедансной гоаницы, следовательно, для эффективного возбуждения поверхностной волны вертикальный размер источника должен быть бесконечно большим. Этим объясняется малая доля мощности, переходимая в поверхностную волну в случае, рассмотренном Ценеком. Из этого факта следует, что эффективные возбудители поверхностной волны могут быть практически созданы только при больших замедлениях (v >> 1,2).

Во втором случае фазовое распределение между источниками должно соответствовать изменению фазы поля поверхностной волны

Рис. 3. Способы возбуждения поверхностных волн

а - антенна осевого излучения с рупорным возбудителем; б-антенна осевого излучения с возбуждением поверхностной волны по второму способу; в - антенна осевого излучения

со щелевым возбудителем

вдоль направления распространения по закону kjx. Возбуждение при этом тем эффективнее, чем больше длина, занимаемая источником.

Таким путем поверхностные волны возбуждаются в электронных приборах СВЧ, где скорость потока электронов подбирается примерно равной скорости распространения волны.

Практически линии поверхностной волны чаще всего возбуждаются рупорным возбудителем (рис. 3, а). Импедансная поверхность заходит в рупор, где высота ребер или толщина диэлектрического слоя плавно снижается до нуля. Длина рупора колеблется от I до 31 в зависимости от замедления, которое определяет и высоту рупора. Высота рупора должна быть такой, чтобы поле ослабевало у верхней грани рупора по сравнению с полем у импедансной границы в несколько раз. При замедлении у = 2, рупоре длиной 31 и при максимальном расстоянии верхней грани рупора от ребристой поверхности оказывается возможным перевести в поверхностную волну более 90% мощности, подаваемой на вход возбудителя. В случае диэлектрической поверхности возбуждение может осуществляться открытым концом волновода без зазора между диэлектриком и верхней стенкой волновода. В линии с малым замедлением целесообразно поверхностную волну возбуждать на участке с большим замедлением и после возбудителя плавно уменьшать импеданс до требуемого значения.

В ряде случаев, например при создании невыступающих антенн поверхностных волн, рупорные возбудители описанного типа

оказываются неприемлемыми, так как выступают за пределы импе-дансной поверхности. Тогда используются возбудители, работающие по второму принципу. Конструктивно такой возбудитель для диэлектрической линии может выполняться в виде рупора или другого источника параллельных лучей, заполненного диэлектриком (рис.

3, б). Угол между импедансной границей и пучком лучей выбирается так, чтобы на границе фаза излученного возбудителем поля менялась по закону k-x. В ребристой линии и диэлектрическом слое с металлической подложкой поверхностная волна может возбуждаться щелевым возбудителем (рис. 3, в). Разность фаз между двумя щелями должна равняться kyT, где Т - шаг щелей, не превышающий по величине половины длины волны в диэлектрике. Требуемая разность фаз создается подбором фазовой скорости в питающем волноводе и размещением щелей на нем.

Возможны, разумеется, возбудители, использующие оба принципа, в этом случае источники поля располагаются в некотором объеме.

4. Антенны поверхностных волн

Линии поверхностных волн и замедляющие структуры широко используются для построения различных типов антенн. Как было показано, поверхностная волна над плоской импедансной бесконечной поверхностью с чисто индуктивным импедансом распространяется без потерь и, следовательно, не излучает электромагнитную энергию. Для использования такой линии в качестве антенны необходимо поместить в поле волны излучатели энергии. В случае ребристого волновода простейшими излучателями являются щели, прорезанные на узкой или широкой стенке волновода (рис. 4). Интенсивность излучения резонансной одиночной щели в волноводе характеризуется проводимостью g. Излучаемая мощность определяется по формуле

Р -

* изл -

(15)

Эквивалентная схема щели состоит из двух отрезков линии электрической длиной 6 и 02, между которыми включена шунтирующая проводимость. Для продольной щели 9i = - = 0. Для поперечной щели 9i = - 6 = jt/2. Для наклонной и смещенной щелей на широкой и узкой стенках волновода Qi = - 02 может изменяться от -л/2 до 4- л/2. Продольная щель в волноводе возбуждается поперечными токами, и поэтому проводимость щели возрастает с увеличением смещения. Проводимость поперечной щели на широкой стенке волновода уменьшается с ростом смещения, а на узкой - с приближением к верхней стенке волновода. Наклонно-смещенная щель имеет две степени свободы, поэтому подбором угла наклона и смещения можно получить заданную проводимость и электричес-

кую длину 01. В случае «открытой» ребристой структуры щели могут быть прорезаны в металлическом листе, расположенном над структурой. Щель возбуждается только продольными токами. Связь с волноводами регулируется углом наклона и расстоянием листа от ребристой поверхности. В качестве излучателей могут использоваться также вибраторы, помещенные в поле поверхностной волны.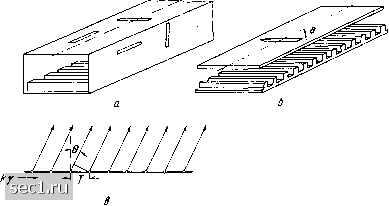

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

Рис. 4. Щелевые излучатели в поле поверхностной волны

о - способы размещения щелей в ребристом волноводе; б - щель в металлической плоскости над «открытой» ребристой структурой; в - система излучателей в поле поверхностной волны

например в диэлектрике. В случае диэлектрической линии вибраторы могут укрепляться на импедансной границе.

Для формирования диаграммы направленности в поле поверхностной волны помещается система излучателей с постоянным шагом Т (рис. 4). Максимум диаграммы направленности формируется в направлении, где сигналы от всех излучателей приходят в фазе. Для выполнения этого условия достаточно, чтобы сигналы от двух соседних излучателей приходили в фазе, т. е. чтобы выполнялось условие

kTxxiQ - k-T =2пп, (16)

где первый член равен разности фаз волн, идущих от первого и второго излучателей в направлении 0; второй член - разность фаз волн, возбуждающих излучатели; п = 0; +1; ±2;...

Из (16) получаем уравнение, которое обычно называют уравнением качания:

si п 0 = т Н- га -.

(17)