2. ДИАГНОСТИРОВАНИЕ БЕЗ ВОССТАНОВЛЕНИЯ

Выбор модели взаимодействия элементов в процессе проверки системы предопределяет в значительной степени сложность реализации и основные характеристики алгоритмов диагностирования (их быстродействие, занимаемый объем памяти, возможности структуризации и т. п.). Поэтому при разработке отказоустойчивых систем естественным является стремление к использованию наиболее простых моделей, в которых функциональные особенности элементов системы не играют существенной роли при анализе технического состояния системы в целом.

Такой подход позволяет создавать достаточно универсальные алгоритмы и программы диагностирования и контроля, применимые для широкого класса реальных систем. Это послужило одной из основных причин широкого распространения Р-моделей взаимодействия, которые достаточно просто и полно описывают диагностирование в многомашинных распределенных системах, построенных на основе микро-ЭВМ и микропроцессоров.

Действительно, при достаточно надежных связях между элементами системы каждый из них может устанавливать связи с другими элементами и подавать на них тесты. Получаемый при проверке результат выполнения теста анализируется контролирующим элементом и принимается решение об исправности. Примером одного из простейших способов такого тестирования является проверка отклика контролируемого элемента по запросу контролирующего элемента с использованием таймера, который входит во многие современные ЭВМ.

Поэтому основное внимание при рассмотрении диагностирования без восстановления уделяется СВК, в которых взаимодействия элементов описываются Р-моделями. Будем называть такие структуры Р-структурами.

Обозначим через (Vi) = {v,- Ч(и,-, Vi)V, VjVt], т. е. множество вершин Vj, соответствующих элементам, контролирующим элемент v.

Теорема 1 [44]. Пусть диагностируемая система S описывается Р-структурой для множества V элементов ( У = п) таких, что для любого (у,, v)E, о,-, VjV, п(/. дЕ. Система S является /-ДС без восстановления тогда и только тогда, когда Vy.-gV, Г"(у,)>.

Данная теорема позволяет определять ДС без восстановления по структурным свойствам графа G - G {V, Е).

Используемое в теореме 1 предположение об отсутствии взаимонаправленных связей, т. е. одновременном наличии

в Р-структуре связей (у,., v,)QE, [Vj, vQE, v,, Vj£V, ограничивает класс рассматриваемых реальных систем.

Во многих существующих микропроцессорных системах, построенных на основе микро-ЗВМ, обычно в процессе функционирования предусматривается возможность выбора в качестве ведущих произвольных микро-ЭВМ. Выбранные микро-ЭВМ могут применяться в качестве контролирующих элементов, причем выбор ведомых микро-ЭВМ, выполняющих функции контролируемых элементов, производится ведущей с использованием схем арбитража и данных о необходимой структурной организации t-RC.

Следовательно, для многих реальных микропроцессорных систем естественным является предположение о наличии двунаправленных связей, т. е. связей

{Vf, Vj)£E, (Vi, v,)£E, Vi,

Основные требования к структурной организации таких систем, обеспечивающей их /-диаг-ностируемость, вытекают из следующей теоремы 44].

Теорема 2. Пусть система S описывается Р-структурой. Система S является /-диагностируемой тогда и только тогда, когда выполняются следующие условия:

1) п> 2/ -fl;

2) Уу,- е V, Г-1 (о,) > /;

3) для каждого О < p<it и каждого XczV \Х \ =п - -2t + p, \ГХ\>р, где rX = [vi](v,. Vj)£E, v,X, £V\X).

Теорема 2 позволяет оценить при заданном количестве элементов п наибольшее количество неисправных элементов /, при котором возможно однозначное определение неисправных элементов в системе. Действительно, непосредственно из условия 1 теоремы 2 следует, что L.(tt- 1)/2 J, где через [ х J обозначено наибольшее натуральное число, не большее х.

Так, например, система, представленная ДГ на рис. 13, является 1-диагностируемой и 2-дкагностируемой без восстановления.

Анализ Р-структур на основе теорем 1 и 2 позволяет оценить /-ДС для заданных значений / и разбиений системы на инцидентные подмножества элементов. Однако в ряде случаев, используя данные об архитектурных особенностях построения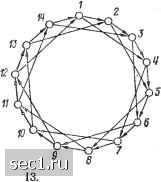

Рис.

Диагностируемая система

системы, удается определить подмножества направленных путей в ДГ системы или оценить связность элементов системы, обеспечиваемую через подмножества других элементов. Наличие таких данных позволяет оценить потенциальные возможности диагностирования в рассматриваемых системах.

Предположим, что ДГ G являегся сильно связным графом, т. е. для любой пары элементов Vi, Vj £ V существует направленный путь связей из одной верщины к другой. Связностью k (G) направленного графа G называется минимальное число вершин ДГ, исключение любой из которых приводит к несвязности графа G. Тогда для Р-структур справедливы следующие два следствия к теореме 2 [44, 51].

Следствие 1. Пусть G = G (У, Е) есть ДГ Р-структуры системы S, состоящей из п элементов, п = \V\. Тогда, если k (G)>- t к п >-2t + 1, то S является -ДС.

Следствие 2. Система S, представленная ДГ G =-- G {V, Е), л = I 1/1, является -диагностируемой, если связь между вершинами с номерами / и / удовлетворяет соотношению / - i = = Ьт (mod n),m=l,2, ипиб представляют собой взаимно npocTiiie числа.

Результаты следствия 2 удобно использовать для построения симметричных диaгнocтиpyeмыx Р-структур.

Оценку диагностических возможностей ДГ можно производить на основе отображения множеств элементов на область натуральных чисел.

Обозначим Р множество всех разбиений множества элементов V системы S на три непересекающихся подмножества (X, Y, Z), удовлетворяющих следующим условиям:

1) \Z\>\;

2) TXY; TX[v vV, HXeA::(x. v)E] - X;

3) T-Z = {v\vV, gzeZ:(y, z)E]-Z;

4) V==X\]Y\]Z.

Пусть К есть функция из множества Р разбиений р на множество натуральных чисел такое, что УрР:

K{p)==\Y\ + \\Z\/2].

Тогда условие f-диагностируемости без восстановления имеет следующий вид.

Лемма 1 [36]. Система S является -диагностируемой тогда и только тогда, когда у/? £ Я : /С (р) > t.

В тех случаях, когда известно минимальное значение К (р), представляется возможным непосредственное определение -ДС. Это значение может быть задано в процессе проектирования отказоустойчивой системы нли получено в процессе перестройки структуры системы.