являются частными случаями соединения Л-угольником (рис. 1.23, а) и Л-лучевой звездой (рис. 1.23,6).

Характер соединения между идеализированными элементами цепи определяет ее топологические (структурные) свойства, для описания которых используют понятия ветви, узла и контура. Ветвь представляет собой участок протекает один и тот же ток. нескольких последовательно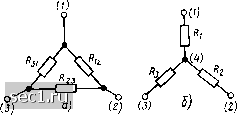

Рис. 1.22, Соединение сопротивлений треугольником (а) и звездой (б)

электрической цепи, вдоль которого Она может состоять из одного или включенных идеализированных двухполюсных элементов. Например, в электрической цепи, схема кото-. рой приведена на рис. 1.21, б, можно выделить ветви, составленные из одного (ветви, содержащие сопротивление R2 или индуктивность L), двух (ветвь, содержащая сопротивление R3 н емкость С) и трех элементов (ветвь с источником напряжения е, сопротивлением Ri и индуктивностью Lj). Так как каждую ветвь можно рассматривать как двухполюсник, то соединения ветвей можно характеризовать теми же терминами, что и соединения идеализированных двухполюсных элементов (параллельное, последовательное и т. д.). Например, электрическую цепь, схема которой изображена на рис, 1.21, б, можно рассматривать как параллельное соединение четырех ветвей: {е, Ri, L}, {R,}, {L,] и {R,C}.

Место соединения ветвей называется у злом, причем место соединения двух ветвей называют устранимым узлом (при соединении двух ветвей текущие через них токи имеют одинаковые значения, поэтому две такие ветви могут быть заменены одной).

Иногда, в частности при автоматизированном составлении уравнений, описывающих процессы в электрических цепях, бывает удобно рассматривать каждый из идеализированных двухполюсных элементов, входящих в моделирующую цепь, в качестве отдель-, ной ветви, при этом необходимо принимать во внимание все узлы, в том числе и устранимые. Будем называть такое топологическое описание цепи расширенным (см, рис. 1.21, а). При сокращенном топологическом описании цепи (см, рис, 1.21,6) группы последовательно включенных элементов рассматриваются в качестве отдельных ветвей и устранимые узлы во внимание не принимаются; таким p„c. 1.23. Соединение сопротивлений Л-уголь-ооразом, количество ветвей ником (а) и Л?-лучевой звездой (б)

2* 35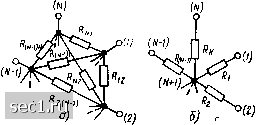

и, следовательно, количество рассматриваемых токов уменьшается (в нашем случае с 7 до 4).

Ветви электрической цепи нумеруют арабскими цифрами, начиная с единицы. Номера ветвей удобно выбирать совпадающими с номерами соответствующих токов, в этом случае номера ветвей на схеме можно не указывать. Узлы электрической цепи нумеруют, начиная с нуля. Порядок нумерации узлов значения не имеет, однако номер «О» удобно присваивать заземленному узлу или узлу, к которому сходится наибольшее число ветвей. Номера узлов условимся обозначать арабскими цифрами в круглых скобках, проставленными около соответствующего узла.

Любой замкнутый путь, проходящий по нескольким ветвям цепи, называется контуром. Например, в электрической цепи, схема которой приведена на рис. 1.21, б можно выделить шесть контуров, образованных ветвями {1,2}, {2,3}, {3,4}, {1,4}, {2,4} и {1,3}. Неразветвленная цепь (см. рис. 1.20, а) содержит только один контур.

Контур характеризуют направлением обхода (порядком перечисленных ветвей), причем каждая ветвь и каждый узел, входящие в контур, проходятся только один раз. Направление обхода контура выбирают произвольно и указывают изогнутой стрелкой (см. рис. 1.21,6).

В отличие от электрических элементов моделирующих цепей ветви, узлы и контуры называются топологическими элементами. Степень сложности исследования процессов в электрических цепях во многом определяется числом топологических элементов. В зависимости от их числа различают простейшие и сложные цепи. К п р о-стейшим цепям относятся одноконтурная (например, см. рис. 1.20, а) и двухузловая (например, см. рис. 1.20, б) цепи, к сложным- цепи с числом узлов более двух и числом контуров более одного.

Понятие о компонентных и топологических уравнениях. Законы Кирхгофа

Математическое описание процессов в электрических цепях базируется на уравнениях двух типов: компонентных и топологических.

Компонентные уравнения (уравнения ветвей) устанавливают связь между током и напряжением каждой ветви. Количество таких уравнений равно числу ветвей, а вид каждого из них зависит только от состава ветви, т. е. от входящих в ее состав идеализированных двухполюсных элементов. При расширенном топологическом описании число ветвей и, следовательно, количество компонентных уравнений равны числу идеализированных двухполюсных элементов, а компонентные уравнения имеют наиболее простой вид - они вырождаются в рассмотренные ранее уравнения, связывающие между собой ток и напряжение на зажимах идеализированных активных и пассивных элементов. Таким образом, уравнения, составленные на основании закона Ома (1.9), (1.10), представляют собой компонентные уравнения для ветви, содержащей один идеализированный пассив-

ный элемент - сопротивление. При сокращенном топологическом опи сании количество компонентных уравнений уменьшается в соответствии с уменьшением числа ветвей, но сами уравнения имеют более сложный вид.

Топологические уравнения отражают свойства цепи, которые определяются только ее топологией и не зависят от того, какие электрические элементы входят в состав ветвей. К топологическим уравнениям относятся, в частности, уравнения, составленные на основании первого и второго законов Кирхгофа.

Первый закон Кирхгофа устанавливает связь между токами ветвей в каждом из узлов цепи: алгебраическая сумма мгновенных значений токов всех ветвей, подключенных к каждому из узлов моделирующей цепи, в любой момент времени равна нулю.

В соответствии с первым законом Кирхгофа для каждого из узлов идеализированной цепи (как при расширенном, так и при сокращенном топологическом описании) может быть составлено уравнение баланса токов в узле

2»„ = 0, (1.37)

где й -номер ветви, подключенной к рассматриваемому узлу. Суммирование токов производится с учетом выбранных положительных направлений: всем токам, одинаково ориентированным относительно узла, приписывается одинаковый знак. Условимся токи, направленные от узла, брать со знаком плюс, а токи, направленные к узлу, - со знаком минус. Такой выбор не носит принципиального характера, а сделан только для удобства последующего изложения, поскольку изменение знаков, приписанных токам, соответствовало бы умножению правой и левой частей (1.37) на -1. Токи ветвей, в которых содержатся управляемые или неуправляемые источники тока и напряжения, учитываются в уравнении (1.37) наравне с токами других ветвей.

Пример 1.1. Составим уравнения баланса токов для всех узлов цепи, схема которой изображена на рис. 1.24, а:

узел (ly - (, - (2 + ("з +(4 = 0;

у:>ел (2).- /з - 1, + (5 - (, - 0; (1.38)

узел (3): - h i «в + i? 0; узел (0): г\ -г (г - U 0.

Если сгруппировать токи, направленные к узлу и перенести их в правую часть уравнения (1.37), а в левой части оставить токи, направленные от узла, то первый закон Кирхгофа можно сформулировать таким образом: сумма мгновенных значений токов, направленных к любому узлу цепи, в любой момент времени равна сумме токов, вытекающих из этого узла. Первый закон Кирхгофа является следствием закона сохранения заряда (уравнения непрерывности) и отражает тот факт, что в узлах идеализированной электрической цепи заряды не накапливаются и не расходуются.