При to = О операторные изображения переходной и импульсной характеристик имеют простой вид

h{t)H ip)lp; (t) ф Н (р). (6.ПО)

Таким образом, импульсная характеристика цепи h*v (О - это функция, изображение которой, по Лапласу, представляет собой операторную характеристику цепи Яу (р), а переходная характеристика цепи hU (t) - функция, операторное изображение которой равно Hkv {р)1р- Выражения (6.109), (6.110) устанавливают связь между частотными и временнйми характеристиками цепи. Зная, например, импульсную характеристику {t), можно с помощью прямого преобразования Лапласа найти соответствующую операторную характеристику цепи

Hk{p)=\ t-thtAt)dt, о

а по известной операторной характеристике Hkv (р) с помощью обратного преобразования Лапласа определить импульсную характеристику цепи

Oo-f/оо

*v(0 = J e"*v(/?)dp.

0„-/оо

Используя выражения (6.109) и теорему дифференцирования (6.51), нетрудно установить связь между переходной и импульсной характеристиками

hHt-io)==~hHt-to). (6.1Ц)

Следовательно, импульсная характеристика цепи равна первой производной переходной характеристики по времени. В связи с тем что переходная характеристика цепи И} (t- to) численно равна реакции цепи на воздействие единичного скачка напряжения или тока, приложенного к цепи с нулевыми начальными условиями, значения функции

{t- to) при /< /„ равны нулю. Поэтому, строго говоря, переходную характеристику цепи следует записывать как {t- to)-l {t - - tg), a не {t - to). Заменяя в выражении (6.111) /i (t - g на h4t to)- 1 {t- to) и используя соотношение (6.103), получаем

h4t-to) = ~lhHt~to)-Ut-to)] = Ht~to) X

1 X-hHt-to) + h{t~to)Ht-to)=Ht~to)hHt-to) +

+ lhHt~to)]t=t,6{t--to). (6.112)

Выражение (6.112) известно под названием формулы обобщенной производной. Первое слагаемое в этом выражений представляет собой производную переходной характеристики при t> > /о. а второе слагаемое содержит произведение 6-функции на значе-

ние переходной характеристики в точке t = t- Если при t = tf, функция h}- (t - tg) изменяется скачкообразно, то импульсная характеристика цепи содержит S-функцию, умноженную на высоту скачка переходной характеристики в точке t = tg. Если функция (t - tg) не претерпевает разрыва при t = tg, т. е. значение переходной характеристики в точке t = равно нулю, то выражение для обобщенной производной совпадает с выражением для обычной производной.

Определение временных характеристик линейных цепей

Для определения переходных (импульсных) характеристик линейной цепи в общем случае необходимо рассмотреть переходные процессы, имеющие место в данной цепи при воздействии на нее единичного скачка (единичного импульса) тока или напряжения. Это может быть выполнено с помощью классического или операторного методов анализа переходных процессов. На практике для нахождения временных характеристик линейных цепей удобно использовать другой путь основанный на применении соотношений, устанавливающих связь меж ду частотными и временнйми характеристиками. Определение времеН ных характеристик в этом случае начинается с составления оператор ной схемы замещения цепи для нулевых начальных условий. Далее используя эту схему, находят операторную характеристику Hkv (р) соответствующую заданной паре; внешнее воздействие на цепь Ху, (t)- реакция цепи ук (t). Зная операторную характеристику цепи и применяя соотношения (6,109) или (6.110), определяют искомые временное характеристики.

При качественном рассмотрении реакции линейной цепи на воздействие единичного импульса тока или напряжения переходной процесс в цепи разделяют на два этапа. На первом этапе (при t]tg, /о+ [цепь находится под воздействием единичного импульса, сообщающего цепи определенную энергию. Токи индуктивностей и напряжения емкостей, Jl2к тoм aimмШ--ШЛJШяшcя на значение, соответствующее поступившей в цепь энергии. На втором этапе (при t > ta+) действие приложенного к цепи внешнего воздействия закончилось (при этом соответствующие источники энергии выключены, т. е. представлены внутренними сопротивлениями), и в цепи возникают свободные процессы, протекающие за счет энергии, запасенной в реактивных элементах на первой стадии переходного процесса. Таким образом, импульсная характе-Т рнстика цепи, численно равная реакции на воздействие единичного им-v пульса тока или напряжения, характеризует свободные процессы в рассматриваемой цепи. Следовательно, при переходе цепи от исходного состояния к первой стадии переходного процесса, законы коммутации не выполняются, а при переходе от первой стадии переходного процес-J саТШ~Второи~ выполняются.

Пример 6.7. Для цепи, схема которой приведена на рис. 3.12, а, найдеч переходную и импульсную характеристики в режиме холостого хода на зажимая 2 -2 Внешнее воздействие на цепь - напряжение на зажимах 1 -Г х (t) - "ii реакция цепи - напряжение на зажимах 2-2 у (t) - Uj.

Операторная характеристика данной цепи, соответствующая указанной паре: внешнее воздействие на цепь - реакция цепи, была получена в примере 6,5:

Следовательно, операторные изображения переходной и импульсной характеристик цепи имеют вид

. Н(р) 1

Л1 (О =

л* (О = Я (р) =

P + RIL

P+RIL

L P+R/L

Используя таблицы обратного преобразования Лапласа (см. приложение 1), переходим от изображения искомых временных характеристик к оригиналам (рис. 6.18, а, б):

hi (/)=е-« (О -6 (t)-R e- L. -

Заменяя в полученных выражениях t на t - находим временные характеристики цепи при te Ф 0:

Отметим, что выражение для импульсной характеристики рассматриваемой цепи (t) могло быть получено и другим путем с помощью формулы (6.112), примененной к выражению для переходной характеристики цепи hM.

Для качественного объяснения вида переходной и импульсной характеристик цепи в рассматриваемом включении, подсоединим к зажимам 1-1 независимый источник напряжения е (t) = Ui(puc. 6.18, в). Переходная характеристика данной цепи численно равна напряжению на зажимах 2-2" при воздей-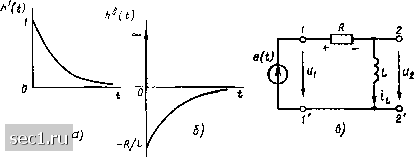

Рис. 6.18. К примеру 6.7

ствии на цепь единичного скачка напряШния е (t) - 1 (t), В, и нулевых начальных условиях. В начальный момент времени после коммутации сопротивление индуктивности бесконечно велико, поэтому при t Iq = О напряжение на выходе цепи равно напряокению на зажимах 1-Г: U2l<=o "ih=o ~ В.

С течением времени напряжение на индуктивности уменьшается, стремясь f нулю при t->- оо. Все это объясняет, почему переходная характеристика начинается от значения (0) - I и стремится к нулю при t оо.

Импульсная характеристика цепи численно равна напряжению на зажимах при приложении к входу цепи единичного импульса напряжения е (t) = ~- 1 - 6 (t), В.