при / 6 ]0 , 0+[ все входное напряжение оказывается приложенным к индуктивности, и ток индуктивности скачком увеличивается от нуля до

- 00

при f > 0+ источник напряжения может быть заменен короткозамыкающей перемычкой, а ток индуктивности плавно уменьигается от (0+) до нуля. Напряжение на индуктивности равно напряоюению на сопротивлении R, поэтому при f > 0+ выходное напряжение цепи изменяется от Uj (0+) = -Rii (0+) = = - RIL до нуля.

§ 6.6. ПРИМЕНЕНИЕ ПРИНЦИПА НАЛОЖЕНИЯ ДЛЯ АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

Определение реакции цепи на произвольное внешнее

воздействие

Наиболее общий подход к анализу переходных процессов в линейных цепях основан на использовании принципа наложения. Внешнее воздействие на цепь х = х Ц)в этом случае представляют в виде линейной комбинации однотипных элементарных составляющих Хи (t):

а реакцию цепи на такое воздействие ищут в виде линейной комбинации частичных реакций у. (t) на воздействие каждой из элементарных составляющих внешнего воздействия в отдельности;

y(.t) = llcc,y,(t).

В качестве элементарных составляющих лг (t) можно выбирать внешние воздействия, описываемые различными классами функций, реакция цепи на которые может быть найдена с помощью рассмотренных ранее методов. Наиболее широкое распространение получили элементарные (пробные) воздействия в виде гармонической функции времени, единичного скачка или единичного импульса.

Метод анализа переходных процессов в линейных цепях, основанный на представлении внешнего воздействия в виде конечной или бесконечной суммы гармонических функций времени, получил название спектрального**.

Определение реакции цепи на произвольное внешнее воздействие по ее переходной характеристике

Рассмотрим произвольную линейную электрическую цепь, не содержащую независимых источников энергии, переходная характеристика которой h} (t) известна. Пусть внешнее воздействие на цепь зада-

*) Этот метод будет рассмотрен более подробно при изучении курса «Радиотехнические цепи и сигналы».

ется в виде произвольной функции л; = л; (t), равной нулю при t<. < /о и непрерывной при всех /, за исключением точки t= t, где х (t) может иметь конечный разрыв (рис. 6.19). Функцию х (t) можно приближенно представить в виде суммы неединичных скачков или, что то же самое, в виде линейной комбинации единичных скачков, смещенных один относительно другого на Дт:

x{t)x (to) 1 {t~Q + 1>Ах (т,). 1 (1 -т,).

(6.113)

Здесь X (if,) - высота ка функции X (0; Дл (Xft) » Дт-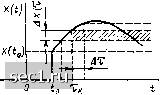

Рнс. 6.19. Представление произвольного внешнего воздействия в виде суммы неединичных скачков

начального скач-dx

высота скачка, подаваемого в момент времени t = (на рис. 6.19 этот скачок заштрихован).

В соответствии с определением переходной характеристики (6.107) реакция цепи на воздействие неединичного скачка, приложенного в момент времени t = t,j, равна произведению высоты скачка на переходную характеристику цепи /i (/ - т). Следовательно.реакция цепи на воздействие, представляемое суммой неединичных скачков (6.113), равна сумме произведений высот скачков на соответствующие переходные характеристики

yit)x(to)h{i-t,) + y,

hit-Xk)Ax. (6.114)

Очевидно, что точность представления входного воздействия в виде суммы неединичных скачков, как и точность представления реакции цепи в видо.(6.114), возрастает с уменьшением шага разбиения по времени Дт. При Дт О суммирование заменяется интегрированием:

y{f)=x(t,)hHt-Q+ hHt-x)dx. (6.115)

Выражение (6.115) известно под названием интеграла Дю-амеля (интеграла наложения). Используя это выражение, можно найти точное значение реакции цепи на заданное воздействие X - X (t) в любой момент времени t после коммутации. Интегрирование в (6.115) осуществляется на промежутке to<.x<.t, причем выражения для х (т) и (t - т) получаются из выражений для х (t) и (t) путем замены f на т и / - т соответственно.

С помощью интеграла Дюамеля можно найти реакцию цепи на заданное воздействие и тогда, когда внешнее воздействие на цепь описывается кусочно-непрерывной функцией, т. е. функцией, которая имеет конечное число конечных разрывов. В этом случае необходимо разбить

11 Зак. 565

интервал интегрирования на несколько промежутков в соответствии с интервалами непрерывности функции х ~ х (t) и учесть реакцию цепи на конечные скачки функции х = х (t) ъ точках разрыва.

• ••••

Пример 6.8. Найдем реакцию цепи на внешнее воздействие, задаваемое функцией X ~ X (t) вида (рис. 6.20)

О при i < 0;

х (t) при О / < /j;

Ч (О при 1 < f < t;

О при t-t.

Разбиваем ось времени на четыре промежутка в соответствии с интервалами непрерывности функции X - X (t).

При / < о реакция цепи у - у (t) тождественно равна нулю (реакция цепи не может опережать по времени внешнее воздействие на цепь).

На участке О <С t <. ti функция х = х {t) непрерывна, поэтому реакция цепи находится непосредственно с помощью выражения (6.115)

у (t) = xi (0) Л1 (0 +

dx, (Т) dx

Л1 (-т) dx.

При ti<. t<. интервал интегрирования ]0, t[ содержит одну точку разрыва функции X (t). Разбивая интервал интегрирования на два промежутка

]0, ]ti, t[ и учитывая реакцию цепи на воздействие скачка функции х (t) в точке t - t, получаем

у (0 = xi (0) Ai (0 + j -5 С-dx+ о

+ [x,(ti)-xi{h)] (t-h) +

Рис. 6.20. К примеру 6.8

При t > интервал интегрирования содер-det

жит две точки разрыва функции х (t). Для определения реакции цепи в этом случае необходимо разбить интервал интегрирования на три промежутка ]0, ti[, Ь, ]<2i 1 " учесть реакцию цепи на скачки функции в точках и t,. Принимая во внимание, что при t> dx [t)!dt - О, получаем

У (0) Л (0-1-

dxi (X)

hi (f-T) di~f [Л-2 (ti)-xi (ti)\ fti (t-h)-\r

dXj (T) dx

Л1 (t~x) dx-x (t) Л1 (/-g.