пиальиой схемы цепи к ее схеме замещения в программах такого типа осуществляется автоматически, с помощью имеющейся в программе библиотеки моделей (схем замещения) всех элементов цепи. При использовании программ анализа цепей более низкого уровня требуется предварительно вручную построить эквивалентную схему цепи. В этом случае в ЭВМ вводят список ветвей идеализированной цепи с указанием характера ветви, ее параметров и ориентации, определяемой порядком перечисления номеров узлов, к которым подключена данная ветвь.

Важнейшим этапом машинного анализа цепей, который наиболее трудно поддается автоматизации, является формирование уравнений электрического равновесия. Рассмотренные ранее алгоритмы составления этих уравнений носят описательный характер, недостаточно формализованы и непригодны для непосредственного применения в программах машинного анализа.

Уравнения электрического равновесия цепи, сформированные любым из методов, можно решать либо в численной, либо в символьной форме. В первом случае находят числовые значения токов и напряжений цепи, соответствующие определенным значения.м параметров элементов и величин, характеризующих внешнее воздействие, во втором - решение получают в виде аналитического выражения, справедливого в определенном диапазоне изменения параметров элементов и величин, характеризующих, заданное воздействие. К настоящему времени наибольшие успехи достигнуты в области численных методов решения уравнений электрического равновесия, которые основаны на хорошо разработанных методах вычислительной математики и легко поддаются алгоритмизации*). Символьные методы решения уравнений электрического равновесия не имеют единой математической базы и развиты в меньшей степени. Имеющиеся программы машинного анализа иепей, реализующие решение уравнений электрического равновесия в символьной форме, основаны на использовании метода сигнальных графов или метода обобщенных чисел и позволяют анализировать только линейные цепи малой сложности. Методы символьного решения нелинейных дифференциальных или алгебраических уравнений вообще не разработаны.

Определяющее влияние на выбор методов численного анализа оказывает уровень развития средств вычислительной техники и соответствующего математического обеспечения. В свою очередь используемые методы численного анализа существенным образом влияют на выбор методов формирования уравнений электрического равновесия. Поэтому на каждом этапе развития вычислительной техники на первый плац выступают свои методы решения уравнений электрического равновесия и соответствующие им методы формирования этих уравнений.

Заключительным этапом машинного анализа цепей является представление результатов. На этом этапе обрабатываются результаты ре-

*) Детально ознакомиться с численными методами решения уравнений электрического равновесия можно при изучении курсов «Высшая математика» и «Вычислительная техника в инженерных расчетах и основы САПР».

шения уравнений электрического равновесия, определяются искомые характеристики цепи, и полученные данные выводятся из ЭВМ. Результаты анализа цепи поступают либо на автоматические алфавитно-цифровые печатающие устройства, либо на дисплеи - визуальные устройства отображения графической и алфавитно-цифровой информации, а при необходимости и на механические графопостроители, которые вычерчивают соответствующие кривые. Современные программы автоматизированного анализа цепей, как правило, организуют работу ЭВМ в диалоговом режиме, при котором пользователь на основе данных предварительного анализа может вводить в ЭВМ директивы, с помощью которых определяется вид анализа, производится изменение схемы исследуемой цепи или параметров ее элементов, задается тот или иной способ представления получаемых результатов.

Программы машинного анализа цепей являются частью современных систем автоматизированного проектирования (САПР) и входят в состав математического обеспечения автоматизированных рабочих мест проектировщика радиоэлектронной аппаратуры. Несмотря на обилие таких программ, постоянно возникает необходимость их усовершенствования или разработки новых программ. Поэтому специалисты в области радиоэлектроники должны четко представлять себе основные принципы, положенные в основу машинных методов анализа цепей.

§ 7.2. МЕТОДЫ ФОРМИРОВАНИЯ УРАВНЕНИЙ ЭЛЕКТРИЧЕСКОГО РАВНОВЕСИЯ, ПРЕДНАЗНАЧЕННЫЕ ДЛЯ ПРИМЕНЕНИЯ В ПРОГРАММАХ МАШИННОГО АНАЛИЗА ЦЕПЕЙ

Компонентные матрицы и компонентные уравнения цепи

Для составления уравнений электрического равновесия цепи с помощью ЭВМ необходимо формализовать исходные данные о топологии цепи и параметрах входящих в нее элементов. Наиболее удобным является представление этой информации в матричной форме. И.звест-но, что топологические свойства цепи полностью определяются ее графом, которому можно поставить в соответствие различные топологические матрицы: матрицу узлов А, матрицу главных контуров В, матрицу главных сечений Q и др. Эти матрицы связаны между собой определенными соотношениями [51 так, что всегда, зная одну из них, можно опредедить любую другую. Наиболее просто с помощью 3BSi формируется матрица узлов, так как при этом не требуется строить дерево цепи и определять соответствующую систему главных контуров или главных сечений.

С помощью ЭВМ можно формировать и компонентные матрицы, применяемые для составления компонентного уравнения цепи в матричной форме. В большинстве программ машинного анализа цепей с целью упрощения и унификации компонентных уравнений ветвей используют расширенное топологическое описание цепи, при которол каждый идеализированный двухполюсный элемент рассматривается в качестве отдельной ветви. Полагая для простоты, что исследуемая

цепь не содержит вырожденных источников, используем один из вариантов расширенного топологического описания цепи, при котором активный двухполюсник, состоящий из идеального источника тока или напряжения и сопротивления, которое можно рассматривать как внутреннее сопротивление соответствующего источника, представляется в виде одной ветви графа.

В зависимости от того, какая из величин (ток или напряжение) выбрана в качестве независимой переменной, компонентные уравнения ветвей, содержащих идеализированные пассивные элементы, могут быть записаны в одной из двух форм: для сопротивления (1.9) или (1.10), для емкости (1.13) или (1.16), для индуктивности (1.22)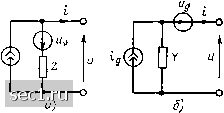

Рис. 7.1. Положительные направ- Рис. 7.2. Схемы замещения обобщенных

ления токов н напряжений вет- ветвей, соответствующих компонентным

вей, содержащих источники напря- уравнениям в форме 2 (а) н в форме Y (б) жения и тока

или (1.23). Принимая, что положительные направления токов и напряжений всех ветвей цепи совпадают, компонентные уравнения ветви, содержащей идеальный источник напряжения (рис. 7.1, а), можно представить в виде

а компонентные уравнения ветви с источником тока (рис. 7.1, б) в

виде

Вводя обозначения sa = йаШ, s-a = adt, где s - оператор

дифференцирования; s- - оператор интегрирования, компонентные уравнения каждой ветви при произвольном внешнем воздействии можно записать (табл. 7.1) либо в форме Z

u = Uv + Z{i-i), (7.1)

либо в форме Y

i=i,+ Y{u-u,). (7.2)

Здесь и, i- напряжение и ток ветви; Y, Z- коэффициенты, определяемые характером входящих в ветвь идеализированных пассивных элементов; i, lu,, ig, Ug - величины, характеризующие внешние