На основании первого закона Кирхгофа можно составить уравнение баланса токов и для так называемого обобщенного узла, который представляет собой часть моделирующей цепи, охваченную произвольной замкнутой поверхностью. В этом случае в уравнении <1.37) алгебраически суммируются токи всех ветвей, входящих в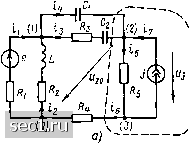

Рис. 1. 24. Примеры схем электрических цепей

обобщенный узел, т. е. токи всех ветвей, пересекаемых указанной замкнутой поверхностью. Так, для обобщенного узла, выделенного пунктирной линией на рис. 1.24, а, уравнение баланса токов

- 1з - U + h = 0. (1.39)

Нетрудно убедиться, что уравнение (1.39) вытекает из уравнений (1.38).

Второй закон Кирхгофа устанавливает связь между напряжениями ветвей, входящих в произвольный контур: алгебраическая сумма мгновенных значений напряжений всех ветвей, входящих в любой контур-моделирующей цепи, в каждый момент времени равна нулю.

В соответствии со вторым законом Кирхгофа для каждого контура можно составить уравнения баланса напряжений ветвей

2«.=0, (1.40)

где k-номера ветвей, входящих в рассматриваемый контур. Суммирование напряжений производится с учетом их положительных направлений и выбранного направления обхода контура. Если положительное направление напряжения ветви совпадает с направлением обхода контура, то оно входит в (1.40) со знаком плюс, в противном случае- со знаком минус. Изменение направления обхода контура, очевидно, соответствует умножению левой и правой частей (1.40) на -1.

Пример 1.2. Составим уравнения баланса напряокений ветвей для всех контуров цепи, схема которой приведена на рис. 1.24, б (номера напряоюений ветвей совпадают с номерами соответствующих токов):

контур /: U, - «2 = 0;

контур 2: + «з = 0; (1-41)

контур 3: и, -i и., 0.

Уравнения по второму закону Кирхгофа можно составить не только для напряжений ветвей, но и для напряжений элементов, входящих в ветви каждого контура. Представляя напряжение каждой ветви в виде суммы напряжений элементов этой ветви и принимая во внимание, что положительное направление напряжения источника э. д. с. противоположно направлению э. д. с, систему уравнений (1.40) можно преобразовать к следующему виду:

щ = еу (1.42)

Здесь «г - напряжения каждого из элементов рассматриваемого контура, за исключением напряжений источников э. д. с; Bj - э. д. с. источников напряжения, действующих в контуре.

Используя (1.42), можно несколько видоизменить формулировку второго закона Кирхгофа: алгебраическая сумма мгновенных значений напряжений на элементах любого контура моделирующей цепи в каждый момент времени равна алгебраической сумме мгновенных значений э.д. с. источников напряжения, действующих в этом контуре. Напряжения на элементах контура и э. д. с. источников напряжения входят в (1.42) со знаком плюс, если положительные направления напряжений на элементах и направления э. д. с. источников напряжения совпадают с направлением обхода контура. В противном случае соответствующие слагаемые в (1.42) берутся со знаком минус.

Пример 1.3. Запишем уравнения баланса напряжений на элементах всех контуров цепи (рис. 1.24. б):

"r2+"l+"c + "r3 = 0; "r-i-"c+"«3 = «-

Второй закон Кирхгофа является следствием закона сохранения энергии и отражает тот факт, что энергия, затраченная сторонними силами на перенос произвольного заряда внутри источников, входящих в контур, равна энергии, затрачиваемой источниками на перенос этого заряда через пассивные элементы контура.

Следует подчеркнуть, что закон сохранения энергии выполняется при переносе заряда по любому замкнутому пути (не обязательно полностью проходящему через ветви цепи). Поэтому уравнения по второму закону Кирхгофа можно составить для любой совокупности элементов, обрающих путь для электрического тока от произвольно выбранного узла (а) электрической цепи к узлу (б) с учетом напряжения между конечными точками этого пути Uao- Например, для ветвей 3 и 2 (рис. 1.24, а), образующих путь для электрического тока между узлами (2) и (0) электрической цепи, уравнение по второму закону Кирхгофа с учетом напряжения Ugo между этими узлами запишется в виде

Wr2 + "г. + "нз + "С2 + «ао = 0.

Для контуров, в которых есть источники тока, уравнения баланса напряжений составляют по общему правилу, причем напряжение на источнике тока учитывается в левой части уравнения (1.42). Так, для контура, образованного ветвями с сопротивлениями j, R3, R, емкостью Cg, источником напряжения е и источником тока / (рис. 1.24, а), уравнение баланса напряжений

«Д1 Н- «R:t + «Н4 + "с2 +- Uj ~ е. t

Так как вид и число уравнений, составленных на основании законов Кирхгофа, не зависят от того, какие элементы входят в состав цепи, а определяются только ее топологическими особенностями, то уравнения баланса токов и напряжений можно применять для математического описания процессов в моделирующих цепях, составленных из двухполюсных элементов любого типа (как линейных, так и нелинейных) при любой форме токов и напряжений независимых источников.

Очевидно, что количество уравнений баланса токов и напряжений равно сумме числа узлов и числа контуров исследуемой цепи. Можно убедиться, что не все из составленных уравнений будут линейно независимыми. Например, любое из четырех уравнений (1.38) может быть получено как линейная комбинация из трех других уравнений: так, уравнение для узла (0) можно получить суммируя уравнения, составленные для узлов (/), (2), (3), и умножая правую и левую части полученного уравнения на -1. Аналогично уравнения (1.41) не являются линейно независимыми.

В то же время на основании законов Кирхгофа для каждой цепи можно составить несколько различных систем линейно независимых топологических уравнений. Например, любые три уравнения из (1.38) и любые два уравнения из (1.41) образуют систему линейно независимых у равнений.

Будем называть системой независимых узлов и системой независимых контуров любые совокупности узлов и контуров цепи, для которых можно составить системы линейно независимых уравнений по законам Кирхгофа. Определение числа независимых узлов и контуров, а также выделение систем соответствующих узлов и контуров являются основными задачами топологии цепей.

Топологические графы электрических цепей

В общем случае граф есть совокупность отрезков произвольной длины и формы, называемых ветвями (ребрами), и точек их соединения, называемых узлами (вершинами). В теории электрических цепей в основном находят применение направлен-н ы е, или ориентированные, графы, у которых каждому ребру приписывается определенное направление, указываемое стрелкой. Различают направленные топологические графы и направленные графы прохождения сигналов. Направленный топологический граф является упрощенной моделью электрической цепи, отражающей только ее топологические (структурные)