повесия цепи по методу узловых напряжений, поскольку токи и напряжения выводов многополюсника могут быть отождествлены с узловыми токами и узловыми напряжениями тех узлов цепи, к которым подключены соответствующие выводы многополюсника. Второй способ задания токов и напряжений многополюсника (рис. 8.3, б) удобен при использовании метода контурных токов. Процессы в многополюснике характеризуются в этом случае напряжениями между выводами многополюсника и токами контуров, образованных сторонами многополюсника и остальной частью цепи. Рассмотренные схемы включения многополюсников будем называть обобщенными (неопределенными).

Анализируя обобщенные схемы, нетрудно установить, что напряжения полюсов многополюсника относительно базисного («ю, Ы20>"-> ыло) не связаны между собой какими-либо соотношениями и могут задаваться независимо. В то же время из второго закона Кирхгофа следует, что напряжения между выводами многополюсника Ui, «2. UN выражаются через напряжения полюсов относительно базисного с помощью соотношений

"i = "ю - "ЛГо.

..................... (8.1)

«лг = МЛГо - «W-l.o-

Из этих выражений следует, что напряжения между полюсами многополюсника не изменятся, если все напряжения полюсов относительно базисного будут изменены на одно и то же значение, следовательно, напряжения между полюсами не зависят от выбора базисного узла. Суммируя уравнения (8.1), получим, что напряжения между выводами многополюсника связаны соотношением

«1 4 «г + ... + Un = 0. (8.2)

Таким образом, только - 1 напряжений между выводами многополюсника могут быть заданы независимо.

Аналогично можно установить, что токи выводов многополюсника il, ij, In не зависят от абсолютных значений контурных токов Iu, hi, i\n, а определяются только их разностьк):

i ~ ll - 221

2 = 22- h:>y

tN -= Inn - hi, и что токи всех выводов связаны соотношением

ij -f + ... -!- i,v - 0. (8.3)

М7

Таким образом, несмотря на то, что все контурных токов /ц, J22, tww являются независимыми, только - 1 токов внешних выводов многополюсника могут быть заданы независимо.

В общем случае каждая пара внешних выводов многополюсника может рассматриваться как его сторона (вход или выход), следовательно, для многополюсника, имеющего внешних выводов, можно выделить С% N {N - 1)/2 сторон (число сочетаний из N по 2). Стороны многополюсника, напряжения (токи) которых могут быть заданы независимо от напряжений (токов) других сторон, называются независимыми. Из соотношений (8.2), (8.3) следует, что у многополюсни-ника, имеющего N внешних выводов, можно выделить не более N - 1 независимых сторон. В частности, четырехполюсник имеет не более трех независимых сторон (см. рис. 8.2).

Основные уравнения и первичные параметры линейных неавтономных многополюсников

Основными уравнениями многополюсни-к а называются соотношения, определяющие связь между токами и напряжениями на его внешних выводах. Коэффициенты, входящие в основные уравнения, называются первичными параметр а-м и многополюсника. В зависимости от схемы включения и того, какие величины выбраны в качестве независимых, а какие - в качестве зависимых переменных, каждому многополюснику можно поставить в соответствие различные системы основных уравнений и соответственно различные системы первичных параметров. Если определитель системы основных уравнений многополюсника не равен нулю, то такая система уравнений называется определенной, в противном случае система основных уравнений является неопределенной. Матрица коэффициентов системы основных уравне-нений, определитель которой равен нулю, называется особенной, или неопределенной, матрицей первичных параметров многополюсника.

Несмотря на то что число независимых основных уравнений многополюсника равно числу его независимых сторон - 1, для описания многополюсников широко используют неопределенные системы основных уравнений, соответствующие обобщенным (неопределенным) схемам включения многополюсников (рис. 8.3), число уравнений в в которых равно числу внешних выводов многополюсника Л. Это позволяет применять достаточно простые методы формирования уравнений электрического равновесия цепей с многополюсными элементами. В то же время, зная неопределенные матрицы первичных параметров многополюсника, легко получать определенные матрицы в любой схеме включения.

Рассмотрим линейный неавтономный многополюсник, находящийся под гармоническим внешним воздействием. Пусть напряжения всех выводов многополюсника относительно базисного задаются с помощью независимых источников напряжения (рис. 8.4, а). В соответствии с принципом наложения ток каждого вывода равен сумме частичных

токов, вызванных действием каждого из независимых источников напряжения в отдельности:

Л =/S)+/1) +...+/(Л) ==Уц 4+£2-1-•••+L V

4 = > + +... + /i) - Yi £1 + £2 +... + Y2N En; (8.4)

/;V = /V> + + ... + /V* = Yn, £1+УЛГ2 E2 + ..- + YNNEN.

Здесь /И - частичный ток i-ro вывода, вызванный действием источника Ё] в режиме, когда все остальные независимые источники напряжения выключены (закорочены).

Коэффициенты уравнений (8.4) - первичные параметры многополюсника - имеют физический смысл входных и передаточных проводимостей, определенных в режиме короткого замыкания, поэтому их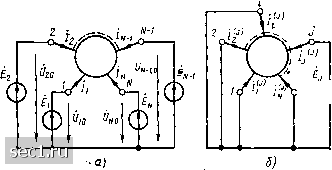

W С)

Рис. 8.4. К выводу основных уравненнй многополюсника в

форме Y

обычно называют параметрами короткого замыкания, или У-п араметрами, многопо люсника. Как видно из уравнений (8.4),

Yjj=lf/Bj- (8.5)

это комплексная входная проводимость многополюсника со стороны зажима / (комплексная входная проводимость между полюсом / и соединенными вместе остальными полюсами), измеренная в режиме, когда все источники напряжения, кроме Ej, выключены (рис. 8.4, б). Аналогично, параметр

Ya = (8.6)

имеет физический смысл передаточной проводимости от полюса / к полюсу i, определенной в режиме, когда все источники напряжения, кроме Ej , выключены (рис. 8.4, б).