Заменяя в уравнениях (8.4) э. д. с. источников соответствующими напряжениями и используя матричную форму записи, получаем

Yji 222 • • • Yj

Yni Yn2--- Ysn

Ого Uno

(8.7)

Уравнения (8.7) будем называть основными уравнениями многополюсника в форме Y. Квадратная матрица

Y21 Y22 •• Y2N

Yni Yn2-- - Ys

в правой части уравнений (8.7), называется неопределенной матрицей проводимостей или неопределенной матрицей К-параметров многополюсника. Ее можно рассматривать как обобщенный параметр многополюсника, устанавливающий связь между вектором токов выводов многополюсника и вектором напряжений этих выводов относительно некоторого базисного узла. Элементы матрицы определяются в соответствии с их физическим смыслом по результатам опытов короткого замыкания, которые могут проводиться как экспериментальным, так и расчетным путем.

Пример 8.1. Найдем неопределенную матрицу Y-параметров полевого транзистора, схема замещения которого по переменному току в режиме малого сигнала изображена на рис. 1.19, б.

Присвоим выводу затвора полевого транзистора номер 1, стока - 2, истока - 3, и составим комплексную схеми замещения (рис. 8.5, а), на которой элементы, входящие в эквива.кнтную схему для мгновенных значений, представлены их комплексными проводимостями: = /мСзи, 2 ~~ iCac, Kg = Gi + + /шСси.

Основная система уравнений рассматриваемого многополюсника в форме Y

содержит девять неизвестных коэффициентов (Y-параметров полевого тран-эистора). Для их нахождения рассчитаем токи транзистора в режимах короткого замыкания на различных парах выводов.

Схема опыта короткого замыкания для определения параметров Уц, Kjj, Уэ1, входящих в первый столбец неопределенной матрицы проводимостей, приведена на рис. 8.5, б. Используя эту схему, найдем частичные токи первого, второ-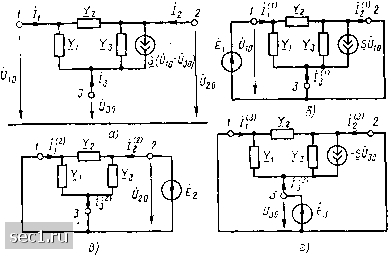

Рис. 8.5. К примеру 8.1

ео и третьего выводов транзистора, вызванные действием управляемого ис, точника напряжения - - Од, включенного между выводом 1 и соединенными вместе остальными выводами транзистора:

Отношения этих частичных токов к э. д. с. вызвавшего их источника напряжения в соответствии с (8.5 и 8.6) являются Y-параметрами полевого транзистора:

Kii = /i»)/£,-Ki \-Y,,

Y, =/i/Ei-.-(S-f К,)-

Аналогичным образом, используя схемы опытов короткого замыкания, приведенные на рис. 8.5, в, г, определим Y-параметры полевого транзистора, входя-Щие во второй и третий столбцы неопределенной матрицы проводимостей:

Yr, 1[ЧК--Y,: Уз /1з)/£з= у;1;

К,, Г,+ Гз; -/."/Ёз.-{Ys+Sy,

Кз2- Д=/£2- -Кз; i:33-- h/Eg-Yi + Ys f S.

Таким образом, неопределенная матрица Y-параметров полевого транзистора имеет вид

~Y, -Kl

Yy= 2

JL-(S + K,)

-(Гз+S)

Y1+Y3+S

Покажем, что не все элементы неопределенной матрицы проводимостей являются независимыми. С этой целью, используя систему уравнений (8.7), найдем сумму токов внешних выводов многополюсника:

/1 + /2 + - + /лГ=(Г11+П1+- + У1)10 +

+ {Yit + Y22 + .- + Yn2) 20 + ... + {Yw + Y2N +... + Ynn) От. (8.8)

Левая часть уравнения (8.8) в соответствии с выражением (8.3) равна нулю, поэтому

(У11 + + . • • + 1) f/io + [Yy, +Jf22 + ... + KW2) f/20 + •.. +

+ (K,jv + F2,v + ...+j:ww)f)wo = 0. (8.9)

В связи с тем что напряжения выводов многополюсника относительно базисного узла можно выбирать независимо, равенство (8.9) должно выполняться при любых значениях и, Uo, Ono- Полагая последовательно равными нулю напряжения всех выводов относительно базисного, кроме одного, заменим уравнение (8.8) системой уравнений

{Yii + Y,i + ... + Yn,)Ui,=0; (n2 + i22 + .-+n-2)fy,o=0;

0iN + Y2N+... + Ynn) Uno=0,

откуда следует, что сумма элементов каждого столбца неопределенной матрицы проводимостей равна нулю.

Если напряжения всех выводов многополюсника относительно базисного одинаковы и равны О (это может быть в том случае, если рее выводы многополюсника закорочены и между ними и базисным узлом включен независимый источник напряжения Ё = U), то их токи должны равняться нулю:

/i = (Iii + >:i2 + -+K,w)f> = 0; h=-iYn + Y2+... + Y2N)U = 0; ............... (8.10)

h(Y Nl-bYN2 + ...+YNN)0=0.

Из уравнений (8.9) следует, что сумма элементов любой строки неопределенной матрицы проводимостей равна нулю. Таким образом, из Л элементов неопределенной матрицы проводимостей только (Л-1) являются независимыми.

Пусть токи контуров, внешних по отношению к многополюснику Задаются с помощью независимых источников тока Ji, j, Jn,