• ••••

Пример 8.5. Определим матрицу Y? биполярного транзистора, включенного по схеме с общей базой, по известной матрице Y-параметров этого транэи-сторч в схеме с общим эмиттером

Дополняя YJJ* строкой и столбцом, соответствующими выводу эмиттера

-{F»v+K()

y(9)

£.22

U вычеркивая строку и столбец, соответствующие выводу базы, получаем матрицу проводимостей биполярного транзистора в схеме с общей базой

Если два каких-либо вывода многополюсника, например с номерами k и N, объединяются в один полюс,которому присваивается номер k, то напряжение этого полюса относительно базисного узла равно иоу а его ток равен сумме токов k-ro и iV-ro выводов. При этом в основной системе уравнений многополюсника (8.7) уравнения для токов -го и N-ro выводов

/лг = Улп i/io + Yn2 L2o +. • • + Fyvft t/fto + • • + Yn.n-1 On-1,0 + Ynn Ono заменяются одним уравнением

kiY ki + Y Ni) 4-{Yja + Yn2) U + ... + Q\ + Yn + Ynm + Ynn)X

XU,g + ... + (Yk,n-l + YN,n-l) UN-i.O.

Следовательно, при объединении -го и yV-ro полюсов в один А-й полюс k-я и Л-я строки неопределенной матрицы проводимостей многополюсника суммируются и становятся k-й строкой, а k-й и N-u столбцы суммируются и становятся k-m столбцом.

•••••

Пример 8.6. Зная неопределенную матрицу проводимостей многополюсника А, приведенного на рис. 8.8, а,

12 3 4

Y у у Y 1д1 Li2 Li3 £л4

у v v у

121 L22 1.23 1-24

-31 ]1з2 Y33 Y3i

Y Y Y Y . 4i La L43 144 J

определяем неопределенную матрицу проводимостей Y,..£ нового многополюсника Б, получающего из исходного в результате объединения полюсов 3 u4 (рис. 8,8, б).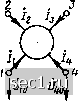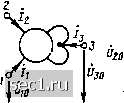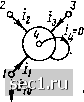

Рис. 8.8. К примерам 8.6 и 8.7

Основные уравнения исходного многополюсника в форме Y имеют вид К = Кп f>io+Ji2 U20 + Y13 Usa + Yii Ош, h =l2i f>io + V22 О20+Y23 f>30 + Y2* 4o

h =141 Uio + У42 Ого + У«, Озо + Ytt Ош-

у мног(1Нолюсника, полученного из исходного путем объединения выводов 3 и 4, напряжение объединенного вывода равно (У30, а ток - сумме пюков третьего и четвертого выводов исходного многополюсника:

/1=2:11 10+2:12 V+iXi H-Ii4) 0;

/2 =2:21 010 +122 t>20 + (123 + 2J4) Ого, /8=(VS1 +V4l)f>iO + (32+>42) f20 + (33 + 34+>4з+44) fSO.

или в матричной форме I

2:13+1:14 2:23+1:24

r88 + i:S4+L8 + 2:44J

Uio Lt/3oJ

Ого lObo.

Таким образом, элементы третьей строки и третьего столбца матрицы Sis действительно равны сумме соответствующих элементов третьей и четвертой строк и третьего и четвертого столбцов неопределенной матрицы проводимо-f;tneu исходного многополюсника.

Если какой-либо вывод многополюсника, например Л-й, не используется при его соединении с остальной частью цепи, т. е. является внутренним узлом многополкэсника, то ток этого вывода

/n =2n I f>io + Yn2 + . •. + Yn.n -I 0 n-u о + Yn w t/wo = 0. (8.16)

Определяя из уравнения (8.16) напряжение Л-го вывода

Uno = -Yn\ VuIYnn-Yn2 Uzq/Ynn - - Yn.n- i Un-i,oIYn,n

и исключая (Jnq из основной системы уравнений электрического равновесия исходного многополюсника, получаем

\ Lnn I \ Lnn /

...+

Y.inX.n,n-

21"

Ynn /

+IY2.N-1

Ynn Y2N Yn,n-i \

Y2N Yn2

Ynn ;

Y.nn

Un-i,o;

(8.17)

/ /v Yn-1.nYni\,; /гл JV-I.ArKW2\ rV I

1n-i = Kiv-i.i---- 110+ Yn-1,2----=\Uio + ...

\ LNN j \~ LNN I

I /л/ Yn-\,nYn,N - \ \ ,-j + rW-l.W-I---- Un-1,0.

Lnn j

Система уравнений (8.17) может быть представлена в матричной форме