
 | |
|
НПО Системы Безопасности (499)340-94-73 График работы: ПН-ПТ: 10:00-19:00 СБ-ВС: выходной  |
Главная » Периодика » Безопасность 0 ... 116117118119120121122 ... 163 где матрица \
YinX.n,n-} Y.fN Y КлГ-1,2 - Yn-i.nYn.n-i Y.NN получается из неопределенной матрицы проводимостей исходного многополюсника путем вычеркивания Л-й строки и Л-го столбца и замены остальных элементов Yjj новыми YI,-, определяемыми с помощью соотношения Y;i = Yij~YiMYNi/Ym. (8.18) Пример 8.7. Зная неопределенную матрицу проводимостей многополюсника, приведенного на рис. 8.8, а (см. пример 8.6), найдем неопределенную матрицу проводимостей \.j д многополюсника, который получается из исходного, если полюс 4 становится внутренним (рис. 8.8, в). Неопределенная матрица проводимостей многополюсника, приведенного на рис. 8.11, в, получается из неопределенной матрицы проводимостей исходного многополюсника путем вычеркивания строки 4 и столбца 4, а также замены остальных элементов новыми, рассчитанными с помощью выражения (8 18): V 2 Ь/в -
Нетрудно убедиться, что сумма элементов любой строки и сумма элементов любого столбца матрицы равны нулю. Рассматривая основные уравнения многополкхника в форме Z, можно установить, что при размыкании какого-либо из внешних по отношению к многополюснику контуров, например k-ro (контурный ток этого контура / становится равным нулю), из неопределенной матрицы сопротивлений многополюсника вычеркивают k-ю строку и k-й столбец. Полученная в результате этого матрица сопротивлений как правило, не является особенной, поэтому основная систе-"1 уравнений многополюсника, один из внешних контуров которого разомкнут, может быть разрешена относительно токов остальных контуров. В ся-личие от неопределенных матриц сопротивлений и проводимостей многополюсника матрицы Z/*) и Y!*>, получаемые из матриц Z,-j и Yjj- путем вычеркивания строки и столбца, будем называть у"корЪченными матрицами сопротивлений и проводимостей многополюсника. При объединении k-vo и N-vo выводов многополюсника в один вывод из неопределенной матрицы сопротивлений исходного многополюсника вычеркивают N-ю строку и Л-й столбец, а остальные элементы исходной матрицы Zj заменяют новыми ZJ/, рассчитанными по формуле Zy = Zij--ZtN Znj/Znn- Если какой-либо из полюсов многополюсника, например k-k, являющийся общим для k-ro и /-Г0 контуров, становится внутренним, то контуры k и I объединяются в один 1-й контур. В этом случае в неопределенной матрице сопротивлений многополюсника вычеркивают k-ю строку и k-й столбец, а к элементам /-й строки и 1-го столбца прибавляют соответствующие элементы fe-й строки и k-ro столбца. Соотношения между элементами неопределенных матриц проводимостей и сопротивлений многополюсника Основные уравнения произвольного линейного неавтономного многополюсника в формах Y и Z описывают зависимости между токами и напряжениями на зажимах этого многополюсника. Очевидно, что коэффициенты основных уравнений (У и Z параметры многополюсника) должны быть связаны между собой соотношениями, позволяющими найти элементы одной из неопределенных матриц многополюсника по известным элементам другой. Определить эти соотношения путем сопоставления выражений для одноименных величин, например токов или напряжений полюсов, полученных из уравнений (8.6) и (8.13), невозможно, поскольку матрицы Zn и Yj; являются особенными и уравнения (8.6) не могут быть разрешены относительно напряжений полюсов, а уравнения (8.13) - относительно токов внешних по отношению к многополюснику контуров. Однако, как было установлено ранее, укороченные матрицы сопротивлений и проводимостей многополюсника не являются особенными и, следовательно, основные уравнения многополюсника, один из выводов которого выбран в качестве общего или один из внешних по отношению к которому контуров является разомкнутым, могут быть разрешены относительно одноименных величин. Пример 8.8. Определим соотношения между Y- и Z-параметрами линейного неавтономного трехполюсника (рис. 8.9, а). Пусть неопределенная матрица проводимостей эпюго трехполюсника известна I 2 3 Хл1 Y.12. His Yjix ILm Y Y Y Lf si 1.32 lasj Выберем любой из полюсов трехполюсника, например полюс 3 в качестве об-щего (рис. 8.9, б) и найдем соответствующую этому случаю укороченную матрицу проводимостей 1 2 1:11 Г12 Основная система уравнений трехполюсника в данной схеме включения имеет /1 = 1 l>io + Vi2 t>2o; h = Yii Ого + У22 Ого- (8.19) Выразим токи полюсов трехполюсника 1, 1 через токи внешних контуров in. /зз (рис. 8.9. в) ii=iix- ii--i»», (8.20) а напряжения полюсов трехполюсника относительно базисного Ui„, Uo через напряокения между полюсами Uio=Ui, иа,= -0з- (8.21) Подставляя соотношения (8.20), (8.21) в (8.19) и решая полученную систему уравнений ~ia3 = Yi0i~YUa относительно Ui, Us, переходим от основных уравнений трехполюсника с общим полюсом 3 (рис. 8.9, 6) к основным уравнениям трехполюсника с разомкнутым внешним контуром 2 (рис. 8.9, в): Oi = Yj, }„l(Yii Yj-Yj, У,г) + Ь Ы/(У п Y„-Y У); Оз = /xi/Olii У«-Ъ Y,i)+l4 8s/(Iu Y,-Yi, Кй) 63 а) Рис. 8.9. К примеру 8.8 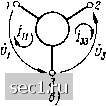 0 ... 116117118119120121122 ... 163 |