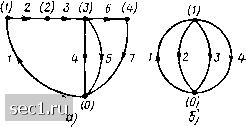Рис. 1.25. Расширенный (а) и сокращенный (б) графы цепи, схема которой приведена иа рис 1 21

свойства. Направленный граф прохождения сигналов представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в электрической цепи. В дальнейшем будем называть направленный граф прохождения сигналов сигнальным графом, а направленный топологический граф просто графом цепи.

Граф электрической цепи строят по ее эквивалентной схеме. Каждую ветвь цепи заменяют при этом отрезком произвольной длины и формы - ветвью графа, а каждый узел цепи преобразуют в узел графа. На ветвях графа стрелками указывают их направления, которые совпадают с положительным направлением токов, протекающих по соответствующим ветвям цепи. Нумерация ветвей и узлов графа та-же, что и нумерация ветвей и узлов схемы. Расширенному топологическому описанию цепи (см. рис. 1.21, а) соответствует расширенный граф цепи (рис. 1.25, а), сокращенному топологическому описанию (см. рис. 1.21,6) - сокращенный (рис. 1.25,6).

Свойства графа не зависят от формы и длины ветвей, а также от взаимного расположения узлов графа на плоскости и определяются только числом ветвей р, числом узлов q и способом соединения ветвей между собой. Графы, имеющие одинаковые количества узлов и ветвей, соединенных между собой одинаковым образом, называются изоморфными (рис. 1.26). Изменяя длину и форму ветвей, а также взаимное расположение узлов графа на плоскости, можно получить бесчисленное множество графов, изоморфных исходному. Такие преобразования графа называются изоморфными преобразованиями. Каждый из вариантов изображения графа, полученный путем таких преобразований, называется его геометрической реализацией.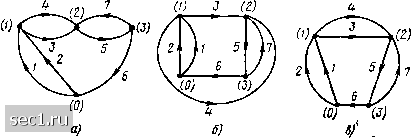

Рис. 1.26. Изоморфные графы

Если узел i является концом ветви /, то говорят, что они и н-ц и д е н т н ы (от англ. incidence - сфера действия, охват). Каждая ветвь графа инцидентна двум узлам. Часть графа, которая наряду с некоторым подмножеством ветвей графа содержит и все инцидентные им узлы, называется подграфом.

Степенью узла называется число ветвей графа, инцидентных данному узлу. На рис. 1.25, а узлы (/) и (4) имеют вторую степень, узлы (0) и (3) - четвертую. i

Графы, изоморфные с точностью до узлов второй степени, называются гомеоморфным и. После удаления из гомеоморфных графов узлов второй степени и объединения инцидентных этим вершинам ветвей гомеоморфные графы становятся изоморфными. Таким образом,

Рис. 1.27. Устранение пересечений ветвей графа с помощью изоморфных преобразований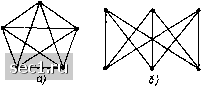

Рис, 1.28 Графы Понтрягина - Ку-

ратовского: а - полный пятиугольник; 6 - двудольный

графы соответствующие расширенному и сокращенному топологическому описанию цепи, являются гомеоморфными. Примером гомеоморфных графов являются графы, изображенные на рис. 1.25.

Планарным (плоским) называется такой граф, который в результате изоморфных преобразований может быть изображен на плоскости без пересечения ветвей. Так, граф, изображенный на рис. 1.27, а, содержит две пересекающиеся ветви, однако он является планарным, так как существует изоморфный ему граф, не имеющий пересечения ветвей (рис. 1.27, б). Можно убедиться, что все графы, содержащие не более четырех узлов, являются планарными.

Непланарный (объемный) граф не может быть изображен на плоскости без пересечения ветвей (рис. 1.28). При удалении из представленных на рисунке графов любой ветви они становятся планарными. Полный пятиугольник и двудольный граф (рис. 1.28) называют также графами Понтрягина-К у-ратовского. Доказано, что произвольный граф является планарным тогда и только тогда, когда он не содержит подграфов, гомеоморфных одному из графов Понтрягина-Курстовского. Электрическая схема, которой соответствует планарный граф, также называется планарной. Непланарной схеме соответствует непланарный граф. Таким же образом вводятся понятия планарной и непланарной идеализированных электрических цепей.

Планарный граф делит плоскость, на которой он изображен, на внешнюю и внутренние области. Внутренние области, ограниченные ветвями графа, называются ячейками или окнами графа. Внешняя по отношению к графу часть плоскости называется базисной Рис. 1.29. Различные пути между вер-Я Ч е й кой. шинами (/) и (3) графа, изображенного

П у т ь - ЭТО подграф, яв- Р*"-

ляющийся последовательностью

соединенных между собой ветвей, выбранных таким образом, что каждому узлу (за исключением двух узлов, называемых граничными) инцидентны две ветви, а граничным узлам инцидентно по одной ветви (рис. 1.29). Каждая ветвь и каждый узел встречаются в пути только один раз.

Замкнутый путь, т. е. путь, у которого начальные и конечные узлы совпадают, называется контуром рис. 1.30). Каждому из узлов контура инцидентны две ветви. Очевидно, что между контурами графа и контурами исходной цепи существует взаимно однозначное соответствие.

Связный граф - это граф, между любыми двумя узлами которого существует, по крайней мере, один путь (см. рис. 1.25-1.28).

Деревом связного графа называется связный подграф, включающий все узлы графа, но не содержащий ни одного контура. Ветви графа, вошедшие в дерево, называются ветвями дерева; ветви, не вошедшие в дерево, называются связями (главными ветвями, хордами). Каждому графу может быть поставлено в соответствие несколько деревьев, отличающихся друг от друга составом ветвей дерева (рис. 1.31). Каждое из деревьев графа, содержащего р ветвей и q узлов, имеет т = q - \ ветвей дерева и п = р - q + I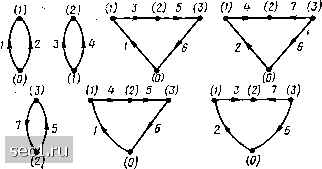

Рис. 1.30. Некоторые из контуров графа, изображенного на рис. 1.26