hi /ssj

Здесь Zij - укороченная матрица сопротивлений трехполюсника, внешний контур 2 которого разомкнут:

Дополняя укороченную матрицу сопротивлений второй строкой и вторым столбцом и вынося из матрицы общий для всех элементов множитель, находим неопределенную матрицу сопротивлений рассматриваемого трехполюсника:

Xbi

I 2 3

-ль. 111+1:12+121+1:22 -(1:11+1:12)

-(Iii+rzi) Zii

Полученные выражения для Z-параметров могут быть упрощены, если принять во внимание, что сумма элементов любой строки и сумма элементов любого столбца матрицы равны нулю:

I 2 3

1 ~"

L1I 1:22 1:12 1:21

Ysz Zs2 Yja

Хлз Ijs

Y Y Y Lijsi 1з1 LuJ

(8.22)

Используя аналогичные преобразования, нетрудно выразить элементы неоп-ределенной матрицы проводимостей трехполюсника через элементы неопределенной матрицы сопротивлений:

1 2 3

£11.33-£lS

£si 1

3 ( £з2 2i2 22

(8.23>

Как видно из выражений (8.22), (8.23), взаимные преобразования неопределенных матриц проводимостей \ij к сопротивлений Zy многополюсника возможны

только в том случае, если укороченные матрицы проводимостей Y* и сопротивлений zf) не являются особенными.

Уравнения электрического равновесия цепей с многополюсными элементами

Уравнения электрического равновесия линейных цепей, содержащих неавтономные многополюсники, формируют с помощью предложенных проф. В. П. Сигорским обобщенных методов узловых напряжений и контурных токов. Основные идеи обо&ценного метода

узловых напряжений состоят в следующем. Если считать, что неопределенная матрица проводимостей трехполюсника известна

1 2 3

Y,y = 2

(8.24)

а внешние выводы трехполюсника /, 2, и 5 подключены соответственно к узлам k, I и S цепи (рис. 8.10, а), то при изменении нумерации столбцов и строк матрицы (8.24) в соответствии с нумерацией узлов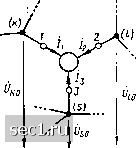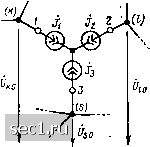

Рис. 8.10. К обоснованию обобщенного метода узловых напряжений

цепи и выборе в качестве базисного узла для отсчета напряжений внешних выводов трехполюсника базисного узла рассматриваемой цепи напряжения внешних выводов трехполюсника относительно базисного будут совпадать с узловыми напряжениями соответствующих узлов цепи, а токи внешних выводов трехполюсника смогут быть выражены через узловые напряжения исследуемой цепи:

k I S

U f 12 fl3 221 22223 31 32 33

Токи и напряжения цепи не изменятся, если вместо выводов трехполюсника к узлам k, I и S подключить источники тока j\, и /3.

1=Л = 1 f>fto+2 +8

/а = 4 bi Om-\-yj2 Vio + Пз .о; (8.25)

Jz - 4 = П1 f/fto + Ув2 0,0 +Yss 0.

Рассматриваемая цепь содержит только идеализированные двухполюсные элементы и для нее можно составить систему узловых

уравнений

Ою Oso

~JiO>

(8.26)

где m - q-l - число независимых узлов цепи, а Y(ij) и jjo - матрица узловых проводимостей и матрица-столбец узловых токов цепи (рис. 8.10, б), которые соответственно равны:

"10

J so ""З J mo -