Выражая токи источников тока Jj, У2. Jz через узловые напряжения цепи (8.25) и перенося соответствующие члены в левую часть уравнения (8.26), получаем

(8.27)

Как видно из (8.27), система узловых уравнений произвольной линейной цепи, содержащей неавтономный трехполюсник, по форме совпадает с системой узловых уравнений вспомогательной цепи, которая получается из рассматриваемой цепи путем исключения этого трехполюсника. Матрица-столбец узловых токов исходной цепи полностью совпадает с матрицей-столбцом узловых токов вспомогательной цепи, а матрица узловых проводимостей рассматриваемой цепи получается из матрицы узловых проводимостей вспомогательной цепи Sj) путем добавления к ее элементам, лежащим на пересечении k-, I- и s-й строк и /- и s-ro столбцов, соответствующих элементов неопределенной матрицы проводимостей неавтономного трехполюсника.

в общем случае исследуемая цепь может содержать не один, а несколько многополюсных элементов с произвольным количеством выводов. Формирование уравнений электрического равновесия такой цепи в соответствии с обобщенным методом узловых напряжений производят в следующем порядке:

1) выбирают базисный узел и нумеруют независимые узлы цепи;

2) изменяют нумерацию столбцов и строк неопределенных матриц проводимостей всех многополюсников в соответствии с нумерацией узлов, к которым подключены выводы этих многополюсников;

3) из неопределенных матриц проводимостей всех многополюсников вычеркивают строки и столбцы, соответствующие тем выводам многополюсника, которые соединены с базисным узлом (элементы этих столбцов и строк не учитывают при формировании узловых уравнений исследуемой цепи);

4) из исследуемой цепи удаляют все многополюсники, для оставшейся вспомогательной цепи, содержащей только идеализированные двухполюсные элементы, формируют систему узловых уравнений;

5) от узловых уравнений вспомогательной цепи переходят к узловым уравнениям исследуемой цепи, для чего последовательно рассматривают все входящие в цепь многополюсники и элементы неопределенных матриц проводимостей многополюсников суммируют с соответствующими элементами матрицы узловых проводимостей вспомогательной цепи.

Очевидно, что количество независимых уравнений электрического равновесия, формируемых с помощью обобщенного метода узловых напряжений, ие зависит от внутренней структуры входящих в цепь миогопвяюсников и определяется только числом независимых узлов внешней по отношению к многополюсникам части цепи.

Отметим, что обобщенный метод узловых напряжений является весьма универсальным и не накладывает никаких ограничений на топологию цепи и количество входящих в нее многополюсных элементов.

Пример 8.9. Составим систему узловых уравнений усилительного каскада на полевых транзисторах, принципиальная электрическая схема которого приведена на рис. 8.11, а. Используем комплексную схему замещения {рис. 8.11, б), где в виде многополюсника представлена модель полевого транзистора по переменному току в режиме малого сигнала.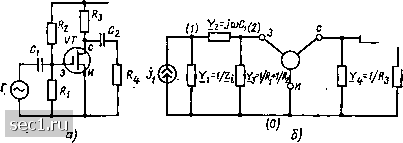

Рнс. 8.11. к примеру 8.9

Изменяя нумерацию столбцов и строк неопределенной матрицей проводимостей полевого транзистора (пример 8.1) в соответствии с нумерацией узлов рассматриваемой цепи, получаем

/и (Сзи+Сзс)

S-/юСзс -(5+/©Сзи)

-/(оСзо Ог + /(о(Сзо + Сси)

-(Gi + /(DCc„)

-/юСэи (S-fGj+/a)Cc„) 54-04-/(0(Сз„4-Се„)

Строка и столбец неопределенной матрицы проводимостей, соответствующие выводу транзистора, соединенному с базисным узлом цепи, могут быть вычеркнуты из матрицы, так как элементы этой строки и этого столбца не будут учитываться при составлении уравнений электрического равновесия.

Составим систему узловых уравнений вспомогательной цепи, которая получается из цепи (рис. 8.11, б) при удалении из нее многополюсного элемента

IГУ1+У2

У,-У, о о

У+Уе

Прибавляя к элементам матрицы узловых проводимостей вспомогательной цепи, расположенным на пересечении столбцов 2, 3 и строк 2, 3 соответствующие элементы неопределенной матрицы проводимостей полевого транзистора, получаем систему узловых уравнений рассматриваемой цепи

Пример 8.10. Используя обобщенный метод узловых напряжений, составим систему уравнений электрического равновесия комбинированного усилителя, со-держащего полевой и биполярный транзисторы (рис. 8.12, а). Комплексная схема замещения усилителя в диапазоне низких частот приведена на рис. 8.12, б.

Неопределенная матрица проводимостей полевого транзистора КТд была найдена в примере 8.1:

XwA-2

/ш (Сзи+Свс) S-/юСзс -(5+/©Сэи)

0L -

-/шСас £{+/•» (Сзс+Сси) -(0+/(вСс„)

-(S+Gi + /(DQ„) 5+0г+/а)(Сз„4-Сс„)