-of я

к iZ)

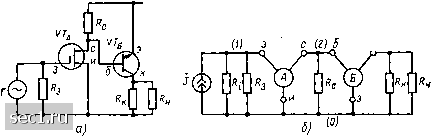Рис. 8.12. К примеру 8.10

Для получения неопределенной матрицы проводимостей биполярного транзистора VT воспользуемся Неопределенной матрицей сопротивлений этого транзистора {см. пример 8.2) и формулами перехода {8.23):

0 3 2

~(R6 + Rm)/T («э + /?б)Дг iRm-R3)/T (/?т-/?к)/Дг -«э/Дг (RK + R3-Rm)/h.

где Aj. = (/?„ + /?б) /?э + («к - /?т) /?б-

Составляя систему узловых уравнений вспомогательной цепи

l/Ri+URa О О

и суммируя элементы неопределенных матриц проводимостей транзисторов с соответствующими элементами матрицы узловых проводимостей этой цепи, получаем окончательно

1 2 3

+ /о)(Сз„+Сзс) 1/У?с+0г+/ш)Сзс+Сс„)+ -/?э/Дг

5-/0)Сз<, +(/?к + о-/?т)/Дг 1/к+! ?..+

О (Rm-R3)JT +(Лэ+/?б)/Аг

Обобщенный метод контурных токов имеет несколько меньшую универсальность, чем обобщенный метод узловых напряжений, и может применяться только при анализе цепей, схема замещения которых является планарной. Формирование уравнений электрического равновесия произвольной линейной цепи, содержащей один или несколько неавтономных многополюсников, в соответствии с обобщенным методом контурных токов выполняется в такой последовательности:

1) нумеруют все контуры, образуемые внутренними ячейками цепи, направление обхода этих контуров выбирают одинаковым - по часовой стрелке;

2) изменяют нумерацию столбцов и строк неопределенных матриц сопротивлений многополюсников в соответствии с нумерацией соответствующих контуров цепи; если одна из сторон многополюсника оказывается не связанной ни с одной из внутренних ячеек цепи, то соответствующей строке и столбцу присваивают номер О, элементы этих строк и столбцов не учитываются при составлении уравнений электрического равновесия цепи;

3) из рассматриваемой цепи удаляют все многополюсные элементы, а точки присоединения полюсов каждого из них к остальной части цепи соединяют между собой, образуя один узел; очевидно, что число контуров полученной таким образом вспомогательной цепи равно числу контуров исходной цепи;

4) используя метод контурных токов, формируют систему уравнений электрического равновесия вспомогательной цепи, состоящей только из идеализированных двухполюсных элементов;

5) от контурных уравнений вспомогательной цепи переходят к контурным уравнениям исследуемой цепи, для чего элементы неопределенных матриц сопротивлений многополюсников суммируют с соответствующими элементами матрицы контурных сопротивлений вспомогательной цепи.

Пример 8.11. Используя обобщенный метод контурных токов, составим систему уравнений электрического равновесия усилительного каскада {см. рис. 8.11, а), комплексная схема замещения которого приведена на рис. 8.13.

Рис. 8.13. К примеру 8.11

Для формирования системы контурных уравнений необходимо определить матрицу Z-параметров полевого транзистора. Воспользуемся для этой цепи неопределенной матрицей проводимостей полевого транзистора {см. пример 8.1) и формулами перехода {8.22):

Д 2 3

Ог + /а)(Сас+Сс„) -(Gt + hC„)

-(S + G(-/юСси) £+<г + /» (Сси+Сэи) S-/шСзс -(5 + /й)Сэ„)

-/соСзо

/о) (Сз„ + Сзс)

где Д = /шСзи {Gi + /ыСэс + /«Сси) 4" /юСзс (S + Gj + /0)0). 372 .

Нумерация сторон многополюсника, а следовательно, и нумерация строк столбцов неопределенной матрицы сопротивлений произведена в соответствии "рис. 8.5 и 8.9. Выберем нумерацию контуров рассматриваемой цепи, как указано на рис. 8.13, и соответственно изменим нумерацию строк и столбцов неопре-%ленной матрицы сопротивлений полевого транзистора

1 3

2 0 3

Сг + /о)(Сзс + Сс„) -(Gi + /o)Cc„) -/шСэс

-(S+G,- + /o)Cch) 5 + Ог+/о)(Сси + Сзи) -/«Сзи

S-/шСзс -(5 + /о)Саи) ;«(Сзи + Сзс)

Удалим из рассматриваемой цепи многополюсный элемент, точки присоединения его выводов соединим между собой и составим систему контурных уравнений для полученной таким образом вспомогательной цепи

Прибавляя элементы неопределенной матрицы сопротивлений полевого транзистора, расположенные на пересечениях строк 2, 3 со столбцами 2, 3, к соответствующим элементам матрицы контурных сопротивлений вспомогательной цепи, получаем систему контурных уравнений исследуемой цепи

-Zi+Z,+ + £3 "Z3 О

£з+[Ог + /й)Х Х(Сзс + Сси)]/Д (5-/й)Сзс)/А

-/соСас/Д

24+[/й)Х Х(Сз„ + Сзс)]/Д

Z4+Z6+

§ 8.2. ОСНОВНЫЕ УРАВНЕНИЯ И СИСТЕМЫ ПЕРВИЧНЫХ ПАРАМЕТРОВ ПРОХОДНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ

Классификация проходных четырехполюсников

Значительное место в теории цепей занимает исследование многополюсников с двумя сторонами (2 X 2-полюсников), которые в отечественной литературе называются проходными четырехполюсниками. В виде проходных четырехполюсников могут быть представлены различные устройства, имеющие две пары внешних зажимов, служащих для подключения источника энергии и нагрузки,