,де Ay = Y22X11 - lizizi - определитель основной системы уравнений в форме У, и сравнивая коэффициенты уравнений (8.29) и (8.34), Z -параметры неавтономного проходного четырехполюсника можно вьфззить через У-параметры того же четырехполюсника:

(8.35)

Соотношения типа (8.35) называются формулами перехо-д а (см. приложение 2). Определители каждой из систем основных уравнений также могут быть выражены через определители или коэффициенты других систем уравнений (см. приложение 3).

Методы определения первичных параметров неавтономных проходных четырехполюсников

Первичные параметры проходных четырехполюсников, как и первичные параметры любых неавтономных многополюсников, могут быть определены в соответствии с их физическим смыслом по результатам опытов холостого хода и короткого замыкания.

Пример 8.12. Определим А-параметры Т-образного четырехполюсника, схема которого приведена на рис. 8.16, а.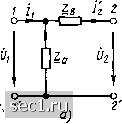

О

Рис. 8.16. К примеру 8.12

Как следует из основных уравнений четырехполюсника в форме А (8.32), параметры All = Ui/Ul Q « = /i/t2l/ o определяются в режиме холостого хода (рис. 8.16, б), а параметры = i(/2-о " -~ VJ2ly о - в режиме короткого замыкания на зажимах 2-2 (рис. 8.16, в). Из этих ехем видно, что в режиме холостого хода

U,==Ui==Ei; l\ = Ui/Z = EjZa,

о в режиме короткого замыкания

/; ==UjZb = Ei/Zb; hUi (l/Za+l/Zb) = (Za + Zb) ej{Za Zb).

Используя полученные соотношения, находим

A, = E\ (Z+Zb) Zb/iZa Zb £i)= 1+Zb/Zo

A==.

1 Zb

1/Z„ 1 + Zb/Z„

Пример 8.13. Определим Н-параметры Т-образного четырехполюсника, схема которого изображена на рис. 8.17, а.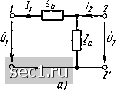

Рис. 8.17. к примеру 8.13

Из основных уравнений четырехполюсника в форме Н (8.30) следует, что параметры четырехполюсника Яц = Ujlj{. и = hhl,-, „ определя-ются в режиме короткого замыкания на зажимах 2-2, а параметры Н =

= UJUil; „ и Н22 = IjUl- в режиме холостого хода на зажимах

11 = 0 - /1 = 0

1-/. Выполняя опыты короткого замыкания {рис. 8.17, б) и холостого хода (рис.

8.17, в), находим матрицу И-параметров рассматриваемого четырехполюсника:

Zp; 1

Пример 8.14. Определим Z-параметры симметричного мостового четырехполюсника (рис. 8.18, а).

Анализируя основную систему уравнений четырехполюсника в форме Z (8.29), нетрудно установить, что параметры Z = Ujl\. и Zjj =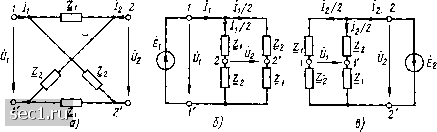

Рис. 8.18. К примеру 8.14

определяются в режиме холостого хода на зажимах 2-2 (рис. 8.18, б), а параметры 12 Ujl\- и и Z22 = и2/11 j - в режиме холостого хода на зажи-дд. /-/ (рис. 8.18, в). В,режиме холостого хода на зажимах 2-2

l\ = 2U\l(Zy+Z2); и2 = (Zj-Zl) /1 /2, а 8 режиме холостого хода на зажимах 1-

ll = 2U,/(Z,+Z2); lJi(Z2-Zy) ISl.

откуда

(Z, + Z,)/2; (Z,-Zi)/2 (Z,-Zi)/2; (Z2 + Zi)/2

Рассмотренный метод определения первичных параметров проходных четырехполюсников является наиболее универсальным и широко используется на практике. В то же время процесс нахождения первичных параметров проходных четырехполюсников во многих случаях может быть существенно упрощен за счет использования ряда других, менее общих методов. В частности, если для рассматриваемого четырехполюсника известны первичные параметры, образующие систему любого типа, то для определения первичных параметров любого другого типа целесообразно воспользоваться формулами перехода.

Пример 8.15. Определим А-параметры Т-образного четырехполюсника (см. рис. 8.17 d).

Используя известные значения Н-параметров данного четырехполюсника (см. пример 8.13) и применяя формулы перехода (см. приложение 2), находим

1=-Я22/Я2, = 1/Z„; 42=-1/Я2, = 1.

Пример 8.16. Определим А-параметры симметричного мостового четырехполюсника, рассмотренного в примере 8.14. Используя формулы перехода, находим

An = ZiJZi=(Z+Zi)l(Z2-Z{)-, 2=A/Z2i = 2Zi Z2/(Za-Zi); Л„ =

= l/Zi =2/jZ2-Z,);j422=jZ22/Z2i=(Z2 + Zi)/(Z2-Zi).

Первичные параметры несложных четырехполюсников могут быть определены путем преобразования соответствующих уравнений электрического равновесия непосредственно к одной из форм записи основных уравнений четырехполюсника (8.28)-(8.33).

Пример 8.17. Определим А-параметры идеального трансформатора, комплексная схема замещения которого приведена на рис. 2.54, а.

Токи и напряжения первичной и вторичной обмоток идеального трансформатора связаны соотношениями (2.182), представляющими собой не что иное, как основные уравнения трансформатора в форме А. Сравнивая уравнения (2.182) и (8.32). находим

. [!/«; О

I -[ 0; п