Примерке. 18. Определим Z-параметры четырехполюсника рис. 8.19, а. Подключая к зажимам 1-/ и 2-2 источники напряжения = 0, Е =5 = и доставляя систему уравнений электрического равновесия полученной цепи А (рис. 8.19, б) по методу контурных

Рис. 8.19. К примеру 8.18

(Zi + Z,) /11 +Zj /22 = £г;

(Z2 + z3) /22 + 2 /jl=/2-z4 /ц,

2 где /ц = /,; /22 = I, получаем

U,(Z-]-Z,) l\ + Zj,;

U2=(Z2 + Z,) /,+ (Zj + z3) /2;

откуда

Zi+Zj; Z2

22 + z4; £2 + 23

Если для какого-либо многополюсника известна неопределенная матрица проводимостей или сопротивлений, то параметры проходного четырехполюсника, который получается из данного многополюсника при определенном выборе пар входных и выходных зажимов, могут быть определены с использованием ранее рассмотренных свойств неопределенных матриц первичных параметров неавтономных многополюсников.

Пример 8.19. Определим Y-параметры проходного четырехполюсника, схема которого изображена на рис. 8.20.

Сравнивая схемы, приведенные на рис. 8.20 и 8.5, устанавливаем, что проходной четырехполюсник исследуемого типа получается из многополюсника, рассмотренного в примере 8.1, при 1/30 = О uS = У. Следовательно, матрица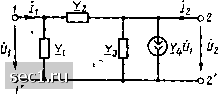

Рис. 8.20. К примеру 8.19

Y-параметров проходного четырехполюсника может быть получена из неопределенной матрицы проводимостей такого многополюсника путем вычеркивания строки и столбца, соответствующих выводу 3, и замены S на У:

Y.-y, К2 + к3

мно-

•••••

пример 8.20. У неавтономного многополюсника (рис. 8.21, а) выделены две пары зажимов 1-5 и 2-3. Найдем Z-параметры полученного проходного четырехполюсника (рис. 8.21, б) по известной матрице сопротивлений исходного гополюсника*)

. . . .

±11 ±12 fl3 £l4 ±15

7* 7* 7 7* 7*

±21 ±22 ±23 24 ±25

Z - 7* 7* 7* 7* 7*

±У ~ 31 ±32 ±33 ±34 ±35

7* 7* 7* 7* 7*

±41 ±42 ±43 ±44 ±45

7* 7* 7* 7* 7*

±51 ±:52±53±54 ±55

Из сравнения рис. 8.21, а, б видно, что проходной четырехполюсник получается из многополюсника путем размыкания сторон 2, 4 и 5. Матрица Z-параметров многополюсника с разомкнутыми сторонами получается из неопределенной матрицы сопротивлений при вычеркивании столбцов и строк, соответствующих разомкнутым сторонам:

,.(2) (4) (5)

£l3

L ±31 ±33 J

Основная система уравнений многополюсника с разомкнутыми сторонами 2, 4, 5 имеет вид

t/,=iii

1+13 33I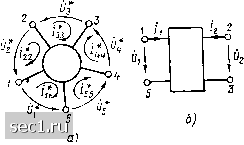

з- £31 П+ЗЗ 33-

Рис. 8.21. К примеру 8.20

Учитывая соотношения между токами и напряжениями проходного четырехполюсника и исходного многополюсника с разомкнутыми сторонами О* =--= Ul, Ut = -U2, ЛI = /1; /33 = -/2. получаем

(/i = 2 I Ii -Z[3 /2;

ri:33 2 •

откуда

-£;з

-±33 J

Первичные параметры линейного неавтономного проходного четырехполюсника могут быть выражены через элементы матриц контурных сопротивлений или узловых проводимостей. Рассмотрим произвольный линейный неавтономный проходной четырехполюсник (рис. 8.22). Используя теорему компенсации, заменим ветви, подклю-

*) Все величины, относящиеся к исходному многополюснику, выделены Звездочкой.

ченные к зажимам 1-1 н 2-2, идеальными источниками напряжения El = и\ и £2 = 2- Выберем дерево полученной цепи таким образом, чтобы ветви, содержащие источники напряжения, не вошли в состав ветвей дерева, и пронумеруем независимые контуры так, чтобы контур, в состав которого входит источник £1,ыл первым, а контур с источником £2 - вторым (общее число контуров равно п). В связи

с тем что рассматриваемый 2 четырехполюсник неавтоном-

ный и, следовательно, не содержит неуправляемых источников энергии, контурные э. д.с. всех контуров, кроме первого и второго, равны

нулю (£11 =1. £22 = £г,

£33 = 44 ••• = пп = 0).

Составляя систему контурных уравнений рассмат-относительно токов первого ti = и

Рис. 8.22. К определению У-параметров четырехполюсника через элементы матрицы контурных сопротивлений

(8.36)

риваемой пени и решая ее второго /22 = Л контуров, получаем

А = Лц £, /А -f ЁJ = Д11 UJA + Д2102/Д; /2 = Д,2 Ё,/А + Д22 Яг/Д = Д12 f>i/A + Даг г/Д-

Из уравнений (8.36) и (8.28) следует, что У-параметры произвольного линейного неавтономного проходного четырехполюсника могут быть выражены через определитель Д и алгебраические дополнения элементов Д;, системы контурных уравнений четырехполюсника:

Гп=Дп/Д; Г.2=Д.л/А;

(8.3/)

Г22=Д22/А.

Аналогичным образом, применяя метод узловых напряжений, Z-параметры неавтономного проходного четырехполюсника могут быть выражены через определитель Д и алгебраические дополнения элементов Д; матрицы узловых проводимостей:

Z„==Au/A; Zi2 = A2i/A;

Za, = Д12/Д; Z22 = Д22/А.

Используя соотношения (8.37), (8.38) и формулы перехода (см. приложение 2), любой из первичных параметров проходного четырехполюсника можно выразить либо через элементы матрицы его контурных сопротивлений, либо через элементы матрицы его узловых проводимостей.

Рассмотренный метод не нашел широкого применения для практического определения первичных параметров четырехполюсников, од-, нако является весьма удобным при исследовании общих свойств матриц первичных параметров проходных четырехполюсников. В частности, анализируя выражения (8.37), (8.38), можно установить, что