Схемы замещения неавтономных проходных четырехпол юсников

ранее было установлено, что соотношения между токами и напряжениями на зажимах любого линейного неавтономного проходного четырехполюсника независимо от числа входящих в него элементов и способа их соединения могут быть описаны системой из двух уравнений, содержащих в общем случае не более четырех независимых коэффициентов. Убедимся, что такой системе уравнений всегда можно поставить в соответствие идеализированную электрическую цепь, содержащую не более четырех элементов, параметры которых могут быть выражены через независимые коэффициенты основной системы уравнений четырехполюсника (условное графическое изображение такой цепи называется эквивалентной схемой или схемой замещения четырехполюсника).

Таким образом, каждому линейному неавтономному проходному четырехполюснику может быть поставлена в соответствие эквивалентная схема, содержащая не более четырех элементов.

Для каждого четырехполюсника можно построить несколько эквивалентных схем, имеющих различную топологию и отличающихся как типом изображенных на них элементов, так и значениями их параметров. Выбор той или иной эквивалентной схемы определяется удобством ее применения в рамках решаемой задачи и, в частности, простотой нахождения параметров ее элементов по заданным выражениям для первичных параметров четырехполюсника. Широкое распространение на практике получили Т-образная (см. рис. 8.19, а) и П-образная (см. рис. 8.20) схемы замещения, получившие название канонических схем замещения линейного неавтономного четырехполюсника. Параметры элементов Т-образной схемы замещения связаны с Z-параметрами четырехполюсника соотношениями

2i=Zii Z12; Z2=Zi2; /о соч

(о. Об)

э~21 £121 Z-Z2i 2j2,

а параметры элементов П-образной схемы замещения можно найти по известным значениям К-параметров

У} = 111 +112; I2 = -Il2>

Is = Z 2 +112; I4 = I2. -- (8.59)

с помощью соотношений, полученных в примерах 8.18 и 8.19 соответственно.

Первичные параметры взаимного четырехполюсника связаны между собой соотношениями (8.39), (8.40), поэтому коэффициенты управления управляемых источников напряжения (см. рис. 8.19, а) и тока (СМ. рис. 8.20) равны нулю (Z = О, I4 = 0). Вследствие этого кано-

Шчгские схемы замещения взаимных четырехполюсников {см. /?ыс. 8.14, б в) не содержат управляемых источников тока или напряжения. Пара-

метры элементов эквивалентных схем симметричных четырехполюсников, кроме того, связаны соотношениями

1 =2з =Zii-Zj2 ==Z22 Zi2;

= - 11 + 1j2 = 1j2 -f 12-

T- и П-образные схемы, изображенные на рис. 8.14, б, в, представляют собой канонические схемы замещения взаимных неуравновешенных четырехполюсников. Для взаимных уравновешенных четырехполюсников используют эквивалентные схемы, приведенные на

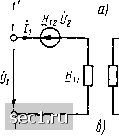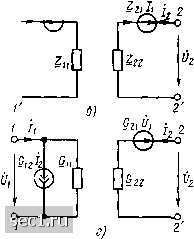Рис. 8.30. Схемы замещения проходных четырехполюсников

рис. 8.14, г, д. Параметры элементов этих эквивалентных схем также рассчитываются по формулам (8.58) и (8.59), а выражения для первичных параметров уравновешенных четырехполюсников совпадают соответственно с выражениями для первичных параметров неуравновешенных четырехполюсников. При решении ряда конкретных задач может оказаться удобным применить эквивалентные схемы четырехполюсника, изображенные на рис. 8.30, параметры элементов которых выражаются через У-, Z-, Я- и G-параметры четырехполюсника соответственно.

Широко применяют в теории цепей (особенно при решении задач синтеза) мостовую схему замещения симметричного четырехполюсника (см. рис. 8.18, а). Параметры элементов этой эквивалентной схемы весьма просто выражаются через Z-параметры четырехполюсника (см. пример 8.14): Zi= Zu - Zi, Z. - Z,j -+ Z,2.

Следует иметь в виду, что комплексным схемам замещения четырехполюсников (см. рис. 8.14, б-д, 8.19, а, 8.20 и 8.30) не всегда можЛ) поставить в соответствие идеализированную электрическую цепь, состоящую из элементов с положительными вещественными параметрами

(С подобной ситуацией сталкивались при знакомстве с эквивалентными преобразованиями цепей со связанными индуктивностями). Несмотря на это , применение таких эквивалентных схем значительно облегчает изучение процессов в непях.

Автономные проходные четырехполюсники

Рассмотрим произвольный линейный автономный проходной четырехполюсник АЧ, схема и параметры элементов которого известны. Заменим внешние по отношению к четырехполюснику ветви источниками напряжения Ё U\, Ё<2= U2A (рис. 8.31, а) и, используя метод контурных токов, найдем токи входных и выходных зажимов четырехполюсника. Если система независимых контуров рассматриваемой пепи выбрана таким образом, что ветвь, содержащая источ-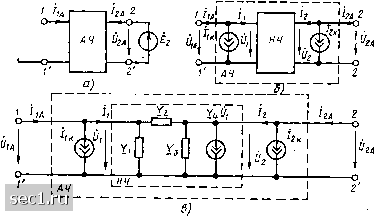

Рнс. 8.31. К определению П-образной схемы замещения автономного проходного четырехполюсника

ник напряжения Ei, входит только в контур /, а ветвь, содержащая источник напряжения £2»- только в контур 2, то искомые токи будут равны контурным токам первого и второго контуров:

/i А = Ац £i/A + Д214/А + /,„; /zA = А12 £i/A + А22 EJA +

4„ = All (£11- £i)/A + A21 (£22 -£2)/A + i Ад £,/Л

(8.60)

/2H = Ai2(£n-£0/A-f A22(£22-£2)/A+ S AjiEjj/A-

,•=3