составляющие контурных токов первого и второго контуров, вызваь ные действием независимых источников, находящихся внутри четырех-полюсника А4.

Как видно из уравнений (8.60), при одновременном закорачиваний источников и £3 токи /lA и /2а равны соответственно /i„ и Ih- Следовательно, и являются токами короткого замыкания внешних выводов автономного четырехполюсника (напомним, что токи короткого замыкания неавтономного четырехполюсника равны нулю). Входящие в уравнения (8.60) коэффициенты Ац/Л, Ai/A, Ац/А и АагД в соответствии с выражениями (8.37) представляют собой У-параметры неавтономного четырехполюсника, который получается из рассматриваемого автономного при выключении всех входящих в него независимых источников. Переходя в (8.60) от э. д. с. Ei, £2 к напряжениям 1а, 2а и используя выражения (8.37), получаем систему основных уравнений автономного четырехполюсника в форме У:

Ла= Кц о хА + УугО-гА + Ак

Аа =21 0\А +222 а. +4к-

Введем токи, равные разности токов выводов автономного четырехполюсника и соответствующих токов короткого замыкания:

А =/lA - Ак = у и 1 а + Kl2 t/2A - Кц Ul + У,2 0; А = Аа- Ан = 1 + 22 U2A = Уп Ul -f У02 U2. (8.61)

Система уравнений (8.61) по форме совпадает с системой основных уравнений неавтономного четырехполюсника, полученного из рассматриваемого автономного четырехполюсника путем выключения всех входящих в него независимых источников и замены Via и Ох на Ui и и,. Используя эту систему, четырехполюснику АЧ можно поставить в соответствие эквивалентную схему, содержащую неавтономный четырехполюсник НЧ, характеризующийся параметрами У, У12,

У21, У22, и два независимых источника тока Ji„ - Ак и - Ак (рис. 8.31, б). Заменяя НЧ канонической П-образной схемой замещения, получаем полную эквивалентную схему автономного четырехполюсника, содержащую в общем случае шесть элементов (рис. 8.31, в).

Если внешние по отношению к автономному четырехполюснику ветви заменить источниками тока Jj = Аа и = Аа (рис. 8.32, а), то, анализируя полученную цепь с помощью метода узловых напряжений, можно получить основные уравнения автономного четырехполюсника в форме Z:

()lA=Zu/lA + Zi22A +1х;

L/2a = Z2, /,а -Ь Z22 /2а + (Угх- (8.62)

Здесь Zii, 2i2, 22i, Z22-первичные параметры НЧ, получающегося

из АЧ путем вьислючения всех независимых источников; Uix и Ux - напряжения холостого хода на входных и выходных зажимах автономного четырехполюсника. В соответствии с уравнениями (8.62) АЧ можно поставить в соответствие схему замещения, состоящую из НЧ л независимых источников напряжения = fУl, fax =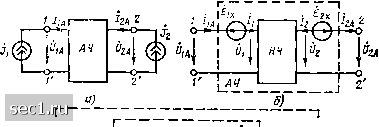

1 IlA О-*-

\ H4

2 -o

-O 2

Рис. 8.32. К определению Т-образной схемы замещения автономного

проходного четырехполюсника

(рис. 8.32, б). Представляя неавтономный четырехполюсник Т-образной канонической схемой замещения, получаем полную эквивалентную схему автономного четырехполюсника (рис. 8.32, в).

Из полученных результатов видно, что автономный проходной четырехполюсник в общем случае характеризуется шестью независимыми параметрами, из которых четыре представляют собой первичные параметры неавтономного четырехполюсника, получающегося из данного автономного путем выключения всех независимых источников, а два параметра являются либо напряжениями холостого хода, либа токами короткого замыкания, измеряемыми при одновременном размыкании или одновременном закорачивании внешних по отношению и автономному четырехполюснику ветвей.

§ 8.3. ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ

И КОМПЛЕКСНЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

НЕАВТОНОМНЫХ ПРОХОДНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ

Комплексные частотные характеристики четырехполюсников при произвольной внешней нагрузке

Несмотря на то что первичные параметры четырехполюсника представляют собой только некоторые комплексные частотные характерис-""Ики, измеренные в одном из предельных режимов (холостого хода

пли короткого замыкания), зная первичные параметры четырехполюсника, образующие любую из систем первичных параметров, можно найти его любые комплексные частотные характеристики при произвольной внешней нагрузке. Если, например, известны значения А-параметров неавтономного проходного четырехполюсника, можно определить его комплексное входное сопротивление со стороны зажимов /-Г Zii (/со) и комплексные коэффициенты передачи по напряжению К21 (/со) и току G.,, (/(й) от зажимов 1-1 к зажимам 2-2 при произвольной нагрузке Z,,.,, подключенной к зажимам 2-2 (рис. 8.33, а).

Рнс. 8.33. К опредслеиню комплексных частотных характеристик проходного четырехполюсника прн произвольной нагрузке

Ток и напряжение на выходных зажимах четырехполюсника в рассматриваемом режиме связаны соотношением /2 = UJZ.,, используя которое, основные уравнения четырехполюсника в форме А (8.32) могут быть преобразованы к виду

и у - An и, + А,2 0!Z„, = (Ли Л12) U/Z,,, = {AnZ„, + Л,.,) А; /, = Л,, и, + А,, U,IZ = (Л21 Z„, + Л22) U,IZ„, =

-(Л 21 z,,2+Л22) ij.

Из уравнений (8.63) следует, что

Z„ ii<o) = Uiii, = (Ли Z„2 + Л2)/(21 Zi + Лг-г);

К.(/«) OlVr = ZI{AiiZja + .2); G-a (/0)) - /2 , = 1 /(Л21Z + Л2.).

(8.63)

(8.64) (8.65) (8.66)

В режиме холостого хода (Zh2 ~ оо) коэффициент передачи четырехполюсника по току равен нулю, а входное сопротивление со стороны зажимов /-/ и коэффициент передачи по напряжению от зажимов /-/ к зажимам 2-2 определяют выражениями

(/о)) =Ли/Ли; K21X {h) == I lAy. (8.67)

В режиме короткого замыкания (Z„2 = 0) коэффициент передачи по напряжению равен нулю, а входное сопротивление и коэффициент передачи по току определяются соотношениями

2п„ (/«) = Л/Лаа; g21k О») = 11А. (8.68)