главных ветвей. При построении деревьев графов электрических цепей в число ветвей дерева обязательно вносят ветви, соответствующие идеализированным источникам напряжения. Ветви графа, соответствующие ветвям цепи, содержащим идеализированные источники тока, в число ветвей дерева не включают.

Добавление к дереву графа любой главной ветви образует контур. Контуры, образованные поочередным добавлением к дереву графа его главных ветвей, называются главными контурами (рис. 1.32). Таким образом, главный контур состоит из ветвей дерева и од-

(Z) 5 (3)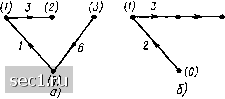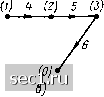

Рис. 1.31. Некоторые из деревьев графа, изображенного на

рис. 1.26

НОЙ главной ветви*). Каждому дереву соответствует своя система из п-р - q -\- 1 главных контуров, причем главные контуры, соответствующие определенному дереву, отличаются один от другого, по крайней мере, одноц ветвью, а именно главной ветвью, входящей в каж-

(!) и (Z) 5 (J) (1) 1+ (2) 5 (3) (О 4 (2) 5 (3) (1) 4 (2) 5 (3)

ХЖ~/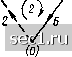

Рис. 1.32. Главные контуры графа (рис. 1.26), соответствующие дереву

(рис 1.31, в)

дый из главных контуров. Каждому главному контуру обычно присваивают номер и приписывают ориентацию (направление обхода), совпадающие с номером и ориентацией соответствующей главной ветви**>.

Сечением графа называется совокупность ветвей связного графа, пересекаемых замкнутой линией (линией сечения) или замкнутой поверхностью (поверхностью сечения), разделяющей граф на две части, причем ни одна из ветвей графа не пересекается дважды. Если удалить из связного графа ветви, образующие сечения, он распадается на две части, одна из которых может быть изолированным узлом.

*) На рис. 1.32 и последующих ветви дерева - сплошные линии, главные ветви - пунктирные.

**) Для большинства задач, рассматриваемых в рамках настоящего курса, нумерация главных контуров может быть выбрана произвольно, независимо от номеров соответствующих главных ветвей,

Каждую из частей графа, лежащую по одну из сторон линии (поверхности) сечения можно рассматривать как обобщенный узел. Так, совокупности ветвей {], 2, 3, 4), {}, 2, 5, 7}, {3, 4, 6), пересекаемых линиями а, б, в соответственно (рис. 1.33), образуют сечения, потому что при удалении каждой из этих совокупностей ветвей граф распадается на две части. Ветви, пересекаемые линией г, не образуют сечения, так как при удалении этих ветвей граф распадается более чем на две части.

Главным сечением графа называется такое сечение, в которое входит только одна ветвь выбранного дерева. Остальные ветви, входящие в главное сечение, являются связями (рис, 1.34). Количество главных сечений равно количеству ветвей дерева, т. е. m = д - 1. Каждому дереву может быть поставлена в соответствие своя система главных сечений, причем главные сечения, соответствующие выбранному дереву, отличаются друг от друга, по крайней мере, одной ветвью - ветвью дерева, входящей в каждое из сечений. Главным сечениям графа присваивают номера и приписывают ориентацию, совпадающие с номером соответствующей ветви дерева и ее ориентацией относительно линии сечения.

Рис. 1.33. К определению понятия Сечение графа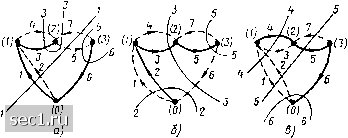

Рис 1.34. Главные сечения графа, приведенного на рис. 1.26, соответствующие деревьям, представленным: а - на рис. 1.31, а: б - на рнс 1.31, б; в - на рнс. I.3I, в

Если одна из частей, на которые граф делится линией сечения, представляет собой изолированный узел, то соответствующее сечение называется каноническим (сечения 5 и 6 на первом из графов, изображенных на рис. 1.34).

Топологические матрицы

Топологические матрицы служат для аналитического описания графов. Такое описание можно представить в виде списка (перечня) ветвей графа с указанием, каким узлам они инцидентны и с какой ориентацией, или с помощью полной матрицы узлов Ас.

Полная матрица узлов (полная матрица инц и денций, матрица соединений, структурная матрица) - это таблица, в которой число столбцов равно числу ветвей графа р, а число строк равно числу узлов q. Номера строк совпадают с номерами узлов (строка с нулевым номером обычно располагается последней), номера столбцов совпадают с номерами ветвей. Элемент матрицы aj, расположенный на пересечении г-й строки и /-го столбца, может принимать значения -1 и 0: aij == -1-1, если ветвь / инцидентна узлу I и направлена от этого узла; а;; = - 1, если ветвь / инцидентна узлу i и направлена к этому узлу; а,-; = О, если ветвь / не инцидентна узлу i. Так, графу, изображенному на рис. 1.26, а соответствует полная матрица инциденций

номера узлов

Нетрудно убедиться, что эта же полная матрица узлов (1.43) соответствует и всем графам, изо.морфным графу, изображенному на рис. ].26, а, в частности графам, приведенным на рис. 1.26, б, в. Таким образом, все изоморфные графы описываются одной и той же полной матрицей узлов. Имея полную матрицу узлов, всегда можно восстановить исходный граф с точностью до изоморфизма.

Число ненулевых элементов в каждой строке матрицы равно числу ветвей, инцидентных соответствующему узлу, т. е. степени узла. В каждом столбце имеется только два ненулевых элемента: -\-\ и -1, так как каждая ветвь инцидентна двум узлам и направлена от одного из них к другому. Сумма всех элементов каждого столбца, а следовательно, и сумма всех строк полной матрицы узлов А равна нулю, т. е. строки полной матрицы узлов являются линейно зависимыми.

На практике обычно используют сокращенную (редуцированную) матрицу узлов А, которая получается из полнай матрицы узлов путем отбрасывания любой из ее строк*). Обычно отбрасывают строку, соответствующую узлу с номером О, который будем называть базисным узлом. Так, отбрасывая строку с номером О у полной матрицы узлов (1.43), получаем сокращенную матрицу узлов А цепи, граф которой изображен на рис. 1.26:

-1 -1 О О

О о

-1 о

-1 о

0 0 о

1 0-1

-1 1 1

(1.44)

*) В дальнейшем будем использовать только сокращенную матрицу узлов А, которую для краткости будем называть матрицей узлов.