Дифференцирующие и интегрирующие цепи

В радиотехнической практике широко используются устройства, напряжение на выходе которых практически пропорционально производной или интегралу от входного напряжения Ui. Такие устройства называются соответственно дифференцирующими или и н-тегрнрующими цепями. В простейшем случае дифференцирование или интегриро-

rw-\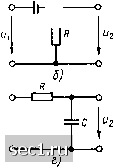

вание напряжения может производиться с помощью пассивных двухэлементных четырехполюсников (рис. 8.39).

1ЛР] s(P) 1г(Р)

UiP) Za(p)\ \ UiP)

Рис. 8.39. Схемы простейших дифференцирующих (а, б) п интегрирующих (в, г) цепей

Рис. 8.40. Обобщенная схема замещспия простейших дифференцирующих и питст-рируюишх цепей

Для определения требований к элементам, входящим в состав дифференцирующих и интегрирующих цепей, рассмотрим обобщенную схему замещения таких цепей, представленную на рис. 8.40. Если напряжение на выходе цепи пропорционально производной от входного напряжения Mj:

где «1 - некоторое действительное число, то в соответствии с теоремой дифференцирования операторные изображения этих величин ip) r=-= U2 п Ul (p) r= Ul при нулевых начальных условиях должны быть связаны соотношением

U-Ap) <ipUi{p).

Следовательно, операторный коэффициент передачи по напряжению дифференцирующей цепи должен быть пропорционален р:

Кц (р) - aip.

Аналогичным образом устанавливаем, что операторный коэффициент передачи по напряжению интегрирующей цепи должен быть пропорционален р

Kzi (р) -- агЯ. где а.2 - постоянный коэффициент.

Полагая, что сопротивление нагрузки обобщенной цепи столь велико, что током /2 (р) можно пренебречь по сравнению с Ii (р), находим выражения для коэффициента передачи обобщенной цепи по напряжению

КМ =-----• (8.122)

Za{p)+Zb(p) l-i-Zbip)/Za(p)

Как видно из выражения (8.122), операторный коэффициент передачи обобщенной цепи может быть пропорционален р или только при

\Z,(p)/ZAp)\ 1. (8.123)

В этом случае для дифференцирующей цепи приближенно выполняется соотношение Z„ (pJ/Z,, (р) = ар, а для интегрирующей цепи

Za ipVZb ip) = «г/р-

Для дифференцирующей цепи выполнение условия (8.123) равносильно тому, что постоянная времени цепи Т/, = L/R (см. рис. 8.39, а) или Т(; = RC (см. рис. 8.39, б) намного меньше длительности дифференцируемого сигнала.

Для интегрирующей цепн условие (8.123) означает, что постоянная времени цепи должна быть значительно больше длительности интервала интегрирования. Из (8.123) также вытекает, что напряжение на выходе «2 простей! шх дифференцирующих и интегрирующих цепей оказывается намного меньшим, чем напряжение на входе Ui этих цепей. Увеличение напряжения может быть достигнуто путем усложнения схем дифференцирующих и интегрирующих цепей, в частности путем применения цепей, содержащих не только пассивные, но и активные элементы.

Гиратор

Гиратором называется идеализированный трехполюсный элемент, комплексные действующие значения напряжений и токов на зажимах которого связаны между собой соотношениями

/i = g2; h--gOi, (8.124)

где g - постоянное вещественное число, называемое коэффициентом гирации или гираторной проводимостью. Условное графическое обозначение гиратора, используемое при построении эквивалентных схем электрических цепей, и условные положительные направления напряжений и токов на зажимах гиратора приведены на рис. 8.41, а. Используя компонентные уравнения гиратора (8.124), можно построить его эквивалентную схему, содержа-•Цую два управляемых напря-

Рис. 8.41. Условное графическое обозначение гиратора (а) и его эквивалентная схема (б)

жением источника тока (рис. 8.41, б), и определить матрицы Y-,Z-А и В-параметров гиратора, включенного с общим полюсом 5:

0; .

\(3) =

0; 0;

В(3) =

g; о

-\ig о

-\lg

(8.125) (8.126) (8.127, (8.128)

Матриц G- и Я-параметров для гиратора не существует. Переходя от (8.125) к неопределенной матрице У-параметров гиратора

нетрудно убедиться, что вид неопределенной матрицы не изменится при изменении нумерации выводов гиратора в направлении по часовой стрелке, т. е. в направлении стрелки, помещенной внутри кружка на его условном графическом обозначении. Таким образом, вид компонентных уравнений гиратора (8.124) не зависит от того, какой из выводов сделать общим, при условии, что нумерацию всех выводов изменяют в показанном стрелкой направлении. Следовательно, цифру 3, указывающую номер общего зажима, в выражениях (8.125) - (8.128) можно опустить.

Некоторые свойства гиратора подобны свойствам идеального трансформатора. Так, токи и напряжения на зажимах гиратора связаны соотношением

(8.129)

подобным выражению (2.184)*), а активная мощность, потребляемая гиратором от источника, равна активной мощности, отдаваемой гира-тором в нагрузку (комплексная мощность, потребляемая гиратором от источника, является величиной, сопряженной с комплексной мощностью нагрузки).

В то же время в отличие от идеального трансформатора гиратор являежя невзаимным идеализированным элементом [Уц ф У, Zi ф Ф Zji, Аа = Дв =7 1) и обладает рядом свойств, не присущих идеализированным элементам других типов. В частности, любой невзаим-

*) При сопоставлении выражений (8.129) и (2.184) необходимо учитывать, что для гиратора и идеального трансформатора выбраны различные направления тока /,.