• ••••

пример 9.2. Определим, является ли функция Я4 (р) = (р + 4)/(р*+ 9р) физически реализуемой в качестве операторной входной функции линейной пассивной цепи.

Непосредственно по виду функции Н{р) устанавливаем, чпю все коэффициен-(ПЫ полиномов N(p) = + 4 н М (р) = р- + 9р вещественны и положительны, И наибольшие и соответственно наименьшие степени этих полиномов отличаются на единицу. Все нули Poi = /2, Рог = -/2 и все по.гюсы pxi = О, Рхг = /3,

= -/3 функции расположены на мнимой оси и являются простыми. Производные функции в нулях

dH, (р)

Р* + Зр + 36

р=±/2 -pЧp--)

-=0.4

и вычеты функции в полюсах

Res Н,(р) = р=0

Res Я,(р) = р=±/з

Р + 4

Зр + 9 р + 4

,Р = 0

Зр2+9

Р=±/з

вещественны и положительны. Вещественная часть на мнимой оси RelW,(P)]p = ,-„ = Re

/а)(9-0))

= 0.

Таким образом, рассматриваемая функция Hf (р) является физически реализуемой в качестве операторной входной характеристики линейной пассивной цепи.

Анализируя критерии физической реализуемости и рассматривая приведенные примеры, приходим к выводу, что если некоторая рациональная функция Н (р) относится к положительным вещественным функциям и, следовательно, является физически реализуемой в качестве операторной входной характеристики линейной пассивной цепи, то обратная ей функция H~ (р) также является физически реализуемой, причем нули функции Я (р) соответствуют полюсам функции Я~1 (р) и наоборот.

Условия физической реализуемости и основные особенности операторных входных характеристик реактивных цепей

Цепи, составленные только из реактивных элементов (емкостей и индуктивностей), представляющие собой частный случай линейных пассивных электрических цепей, называются реактивными Цепями, LC-ц е п я м и, или цепями без потерь.

Необходимое и достаточное условие того, чтобы заданная рациональная функция Н (р) могла быть реализована в качестве входной функции реактивной цепи заключается в том, чтобы Н (р) представляла собой положительную вещественную функцию р и, кроме того, либо Полином N (р) должен быть четным, а полином М (р) - нечетным, либо наоборот. Функция, обладающая такими свойствами, называется Реактансной или реактивной.

Пример 9.3. Определим, является ли функция Я4 (р) = {р + А)1(р -\- 9р) физически реализуемой в качестве операторного входного сопротивления или операторной входной проводимости реактивного двухполюсника.

в примере 9.2 было показано, что такая функция является положительной вещественной функцией комплексного переменного р. В связи с тем что полином N (р) = р + 4 четный, а полином М (р) = р" + 9р - нечетный, функция Я4 (р) относится к реактансным и может быть реализована в качестве оператор, ной входной характеристики реактивного двухполюсника.

Реактансная функция, обладая всеми свойствами положительных вещественных функций, имеет ряд дополнительных особенностей:

1) нули и полюсы ее расположены только на мнимой оси;

2) нули и полюсы чередуются, причем как в начале координат (р = 0), так и на бесконечности {р = ±°°) обязательно находится либо нуль, либо полюс;

3) значения реактансной функции на мнимой оси являются чисто мнимыми и растут с ростом w (в точках непрерывности).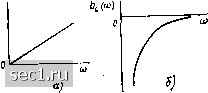

Рис. 9.1. Зависимости от частоты мнимых составляющих комплексного входного сопротивления (д) и комплексной входной проводимости (б) индуктивности

Рис. 9.2. Полюсно-нулевые диаграммы операторного входного сопротивления (а) и операторной входной проводимости (б) последовательной LC-цепи

Рассмотрим операторные входные характеристики некоторых реактивных двухполюсников.

Одноэлементные реактивные двухполюсники. Операторное входное сопротивление индуктивности (р) = = pL имеет нуль в начале координат. При /? оо функция (р) принимает бесконечно большое значение (функция Z (р) имеет полюс на бесконечности). Нули и полюсы Z (р) лежат на мнимой оси (полюс или нуль, находящийся на бесконечности, считается расположенным на мнимой оси). Нули и полюсы чередуются, причем при р = /со значение функции Zl (р) является чисто мнимым: z (/со) = /wL = = jXl (м), и растет с ростом ш: dx {w)/da = L > О (рис. 9.1, а).

Операторная входная проводимость индуктивности Fj, (р) - 1/ /(pL) имеет полюс при /? = О и нуль при р = оо, т.е. нули функции Уг, (р) соответствуют полюсам функции Zl (р) и наоборот. Значения функции Yl (р) на мнимой оси являются мнимыми: (/(о) - = l/(/(oL) = jbL{u)), и растут с ростом (о: dbi, {(o)fd(o =- l/((oL)> > О (рис. 9.1, б).

Поскольку емкость и индуктивность являются дуальными элементами, операторные входные характеристики емкости обладают такими же особенностями, как и операторные входные характеристики индуктивности.

Двухэлементные реактивные двухполюсники. Операторное входное сопротивление последовательной LC-цепи Z {р) = pL + \1{рС) = L {р" + ч>1)1р имеет полюсы в начале координат и на бесконечности и нули, расположенные на мнимой оси:

Pal =- /«о. Ро2 = -/«о. где «о = 1/VlC (рис. 9.2, а) (полюсы и нули, находящиеся на бесконечности, на полюсно-нулевых диаграммах не изображают). Нулям операторного входного сопротивления последовательной LC-цепи соответствуют полюсы операторной входной проводимости этой цепи (рис. 9.2, б)

pL+\l(pC) ~ L(p2 + a)g)

а полюсам операторного входного сопротивления Z (р) - нули Y (р). На мнимой оси значения функций Z (р) и У (р) являются чисто мнимыми

Z (/со) -= jL (ю - (оВ)/(1) = jx (ю); Г(/(й) = -/(й/lL ((0 - (dS)] = jb (ю)

и растут с ростом ю (рис. 9.3, а, б).

Параллельная LC-цепь является дуальной по отношению к последовательной LC-цепи, поэтому операторное входное сопротивление Z (р) = р/с (р + мо) и операторная входная проводимость Y (р) -- = С(р -f (йо) ? параллельной LC-цепи обладают такими свойствами, как и соответствующие им характеристики последователь- ной LC-цепи.

Многоэлементные реактивные двухполюсники. Анализируя операторные входные характеристики произвольных реактивных двухполюсников, нетрудно убедиться, что общее число нулей и полюсов соответствующих функций на положительной мнимой полуоси, включая и внешние (в начале координат и на бесконечности), равно -f 1, где - число независимо включенных реактивных элементов. В зависимости от расположения нулей и полюсов на положительной мнимой полуоси различают операторные характеристики реактивных духполюсников:

1) типа 0-0 (нуль при ю = О и нуль при ю = оо);

2) типа О-X (нуль при ю = О и полюс при ю = оо);

3) типа X-О (полюс при ю = О и нуль при ю = оо);

4) типа X-X (полюс при ю = О и полюс при о» оо).

Для того чтобы определить, к какому типу относятся операторные характеристики заданного произвольного реактивного двухполюсника, достаточно установить, имеются ли между внешними выводами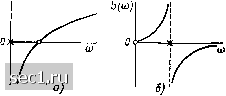

Рис. 9.3. Зависимости от частоты мнимых составляющих комплексного входного сопротивления (а) и комплексной входной проводимости (б) последовательности LC-цепи