этого двухполюсника пути, проходящие только через индуктивности и только через емкости. Если между выводами двухполюсника можно найти путь, проходящий только через индуктивности (сопротивление двухполюсника постоянному току равно нулю), то операторное входное сопротивление имеет нуль в начале координат. Если между выводами двухполюсника отсутствует путь, проходящий только через индуктивности (сопротивление двухполюсника постоянному току бесконечно велико), то операторное входное сопротивление имеет полюс в начале координат. Соответственно, если между выводами двухполюсника имеется путь, проходящий только через емкости, то сопротивление имеет нуль на бесконечности, в противном случае сопротивление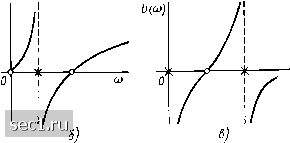

Рнс. 9.4. К примеру 9.4

на бесконечности имеет полюс. Зная особенности операторных характеристик реактивных двухполюсников, можно качественно, по виду схемы, построить частотные характеристики произвольного реактивного двухполюсника.

Пример 9.4. Определим типы частотных характеристик и простроим качественно зависимости от частоты мнимых составляющих комплексных входного сопротивления и входной проводимости реактивного двухполюсника, схема которого изображена на рис. 9.4, а.

Непосредственно по схеме находим, что между внешними выводами двухполюсника имеется путь, проходящий только через индуктивности, и отсутствует путь, проходящий только через емкости. Следовательно, частотная характеристика входного сопротивления относится к типу О-х, а частотная характеристика входной проводимости -к типу х-0. Obwfie число нулей и полюсов, включая внешние, на единицу больше числа реактивных элементов и равно 4. Зависимости от частоты мнимых составляющих комплексных входного сопротивления и входной проводимости рассматриваемого двухполюсника приведены на рис. 9.4, б, в соответственно.

Операторные входные характеристики безыидуктивных и безъемкостных цепей

В отличие от реактивных цепей, полюсы и нули операторных входных характеристик которых расположены только на мнимой оси плоскости комплексного переменного р, полюсы и нули операторных входных характеристик безындуктивных, или RC-цепей, и

безъемкостных, или iL-цепей, располагаются только на (рпцательной вещественной полуоси. Нули и полюсы операторных входных характеристик чередуются и являются простыми (некратными).

Исходя из физических представлений, нетрудно прийти к выводу, что при частоте, равной нулю, сопротивление L-цепи может быть равно нулю или иметь конечное действительное значение; на бесконечна большой частоте сопротивление RL-nenn либо бесконечно велико, либо имеет конечное действительное значение. Следовательно, оператор-

R/L О

-<

-R/L ° 5)

Рис. 9.5. Схемы простейших беземкостных цепей и соответствующие полюсно-нулевые диаграммы операторных входных сопротивлений

ное входное сопротивление безъемкостной цепи не может иметь полюса в начале координат и нуля на бесконечности. Соответственно операторная входная проводимость этой цепи не может иметь нуля в начале координат и полюса не бесконечности. Если операторное входное сопротивление (операторная входная проводимость) безъемкостной цепи на нулевой частоте имеет конечное действительное значение (между входными зажимами цепи отсутствует путь, проходящий только через индуктивности), то ближайшим к началу координат окажется нуль операторного входного сопротивления (полюс операторной входной проводимости). Примеры полюсно-нулевых диаграмм операторных входных сопротивлений простейших RL-nenevi приведены на рис. 9.5, а-г.

Операторное входное сопротивление безындуктивной цепи на нулевой частоте может быть бесконечно большим или иметь конечное действительнее значение, а на бесконечно большой частоте может быть равно нулю или иметь конечное действительное значение. Таким образом, операторное входное сопротивление RC-иепя не может иметь нуля в начале координат и полюса на бесконечности (операторная

входная проводимость не может иметь полюса на нулевой частоте и нуля на бесконечности). Если сопротивление iRC-цепи на нулевой частоте имеет конечное действительно значение (между внешними выводами цепи имеется путь, проходящий только через сопротивления), то ближайшим к началу координат окажется полюс операторного

Рис. 9.6. Схемы простейших безындуктивных цепей и соответствующие полюсно-нулевые диаграммы операторных входных сопротивлений

ВХОДНОГО сопротивления цепи (нуль операторной входной проводимости). Полюсно-нулевые диаграммы операторных входных сопротивлений простей1них iC-цепей изображены на рис. 9.6, а-г.

§ 9.3. МЕТОДЫ РЕАЛИЗАЦИИ РЕАКТИВНЫХ ДВУХПОЛЮСНИКОВ

Метод выделения простейших составляющих (метод Фостера)

Метод Фостера основан на представлении заданной физически реализуемой функции Я (р) в виде суммы простейших функций:

Я (р) Hi (р) + Н,{р) + ... + Ht{p)+ ... + Нп (р),

каждую из которых можно рассматривать как операторную входную характеристику некоторого элементарного одно- или двухэлементного двухполюсника. Если функция Я (р) представляет собой операторное входное сопротивление, то искомая цепь может быть реализована в виде последовательного соединения элементарных двухполюсников, соответствующих каждой из простейших функций Hi (jj). Если Я (р) представляет собой операторную входную проводимость, то искомая цепь реализуется в виде параллельного соединения элементарных двухполюсников, соответствующих каждой из простейших функций Я, (р).