Непосредственно по виду функции Y (р) устанавливаем, что искомый двухполюсник может быть реализован путем параллельного соединения двух последовательных LC-цепей (рис. 9.12). Разлагая Y (р) на простые дроби Y (р) = = р/13 (р + 2)1 + р/(6 (р" + 0,5)], определяем параметры элементов двухполюсника: -= 3 Гн, Ci = 1/6 Ф, La = 6 Гн, Са = 1/3 Ф.

Метод разложения в цепную дробь (метод Кауэра)

В соответствии с методом Кауэра реактивный двухполюсник, обладающий заданной операторной входной характеристикой Я (р), реализуется в виде лестничной цепи, построенной по первой или второй каноническим схемам Кауэра.

Первая каноническая схема Кауэра (рис. 9.13, а) содержит индуктивности в продольных и емкости в поперечных ветвях; вторая каноническая схема Кауэра (рис. 9.13, б) содержит емкости в продольных ветвях, а индуктивности- в поперечных. Первая и последняя ячейки канонических схем Кауэра могут быть неполными - в них могут отсутствовать элементы,

которым на рис. 9.13 присвоены номера 1 и N. Первая каноническая схема Кауэра содержит индуктивность Lj только тогда, когда операторное входное сопротивление цепи имеет полюс на бесконечности. Вторая каноническая схема Кауэра содержит емкость Cj, если операторное входное сопротивление цепи имеет полюс при р = 0.

Как было показано в гл. 2, комплексное (в общем случае операторное) входное сопротивление или комплексная входная проводимость лестничной цепи могут быть представлены в виде цепных дробей (2.133), (2.134), i элементы которых равны комплексным сопротивлениям двухпрлюсников, образующих продольные ветви цепи, и комплексным про]одимостям двухполюсников, образующих поперечные ветви. Если /в первой канонической схеме Кауэра есть индуктивность Lj, то операторное входное сопротивление может быть представлено в виде цепной дроби с элементами типа pai: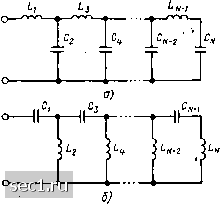

Рис. 9.13. Первая (а) и вторая (б) каио; ннческие схемы Кауэра у

Z{p)=pLi

PL3+...+

pi.Af-l + /(PCw)

1£сли В первой канонической схеме Кауэра нет индуктивности ) операторная входная проводимость имеет полюс на бесконечности) - в виде цепной дроби с элементами типа pai может быть представлена-операторная входная проводимость цепи

Y{p)pCi +-!---

рСз+...-

piN-i + l/(pCw)

Для цепей, построенных по второй канонической схеме Кауэра,. выражения для операторного входного сопротивления

1 N

2(Р) =

\ РСз

рСлг-

•/(рМ

или операторной входной проводимости

у(р)=-4-

-+...+

+ -

4{pLn)

представляются в виде цепных дробей с элементами типа 1/(рРг). Следовательно, если заданная операторная входная функция Я {р) может быть представлена в виде цепной дроби

H{p)Hi{p)-

(9.8)

Я2(Р)+

Яз\(Р)+...

WW ,(P) + 1/[%(P)]

С элементами типа pat или 1/(рРг), где а;, Рг - постоянные действительные положительные коэффициенты, то такой функции может быть поставлен в соответствие реактивный двухполюсник, построенный по первой или второй канонической схеме Кауэра.

Таким образом, реализация реактивного двухполюсника по рассматриваемому методу сводится к разложению заданной реактансной функции Я (р) в цепную дробь с элементами типа pctt или l/(ppj).

Функцию Н (р) = N {р)!М (р) разлагают в цепную дробь вида (9.8) путем последовательного выделения» элементов дроби Я; {р) в результате деления полинома {р) на пол1ом М (р), затем полинома М (р) на остаток от первого деления Oi (р), затем остатка от первого

деления Oi (/?) на остаток от второго деления О, (р), и так далее, до тех пор, пока остаток от последнего деления не будет равен нулю-

М{р) " М(р] М(р)/0, (р)

Яг (Р) +

Ol (Р)/0,(р)

Я,(р)-

з(Р)4-

%{Р)1з (Р)

Для реализации первой канонической схемы Кауэра выбирают ту из входных функций (операторное сопротивление или операторная проводимость), которая имеет полюс на бесконечности, причем члены полиномов N (p)\iM (р) располагают в порядке убывания степеней р.

Для реализации второй канонической схемы Кауэра используют ту из входных функций, которая имеет полюс при р = О, а полиномы N{p) к М (р) располагают в порядке возрастания степеней р. При выполнении деления необходимо следить, чтобы коэффициенты 0(, были положительными. Если в процессе деления какой-либо из коэффициентов а, окажется меньше нуля, то необходимо перейти от расположения полиномов по убывающим степеням р к расположению по возрастающим степеням р. Наоборот, если какой-либо из коэффициентов Рг окажется меньше нуля, то необходимо перейти от расположения полиномов по возрастающим степеням р к расположению по убывающим степеням.

Как и метод Фостера, рассматриваемый метод может быть применен и к синтезу RC-, RL- и iLC-цепей, нули и полюсы операторных входных характеристик которых расположены на мнимой оси и отрицательной вещественной полуоси. Необходимо иметь в виду, что область применимости метода Кауэра несколько уже, чем метода Фостера, так как ряд операторных входных функций, реализуемых с помощью метода Фостера, не может быть представлен как операторное входное сопротивление или операторная? входная проводимость какой-либо лестничной цепи. /

Пример 9.9. Используя метод Кауэра. построим реактивные двухполюсники, операторное входное сопротивление которых

г (р) = (2р + 5р2 + 2)1 (р + р). Ом.

Функция Z (р) имеет поюс на бесконечности и полюс при р == О, поэтому функция Z (р) может быть цспользована как при реализации первой, так и при реализации второй канонических схем Кауэра. Располагая полиномы числителч