ц знаменателя функции Z (р) в порядке убывания степеней р и последовательно выделяя члены вида pat

Р/3

2 ->Оз(р)

р/6 У4(Р)

0-ОЛр) разлигием функцию в цепную дробь

Z, (р)-2р+-

р/3-

и определяем параметры элементов первой канонической схемы Кауэра (рис. 9.14, а): L, - 2 Гн, С, 1/3 Ф. - 9 Гн. С4 = 1/6 Ф.

-Hhr-II

а) 5)

Рис. 9.14. К примеру 9.9

Располагая полиномы числителя и знаменателя функции Z (р) в порядке возрастания степеней р и последовательно выделяя члены вида l/(pPj).

2-1-5р2 Ь2р4 2+2р2

p-f-P" 2

- Z,(p) Р

-*Y,ip)

р»/3 рЗ/ 3

о-*омр)

2р* --0.,(Р)

1 /(6р) (Р)

разлагаем функцию Z (р) в цепную дробь Z(p)-(f)+-

I, бр

и определяем параметры элементов второй канонической схемы Кауэра {рис 9.14. б): Ci = 1/2 Ф, = 3 Гн, Сз = 1/9 Ф, L4 = 6 Гн.

Анализируя примеры 9.7, 9.8,9.9, убеждаемся, что решение задачи синтеза пени по заданной операторной входной характеристике действительно не является единственным. Все четыре полученных в этих примерах двухполюсника (рис. 9.10, 9.12, 9.14) обладают одинаковыми операторными входными характеристиками, но построены по различным схемам из элементов с различными параметрами.

В то же время все четыре полученных двухполюсника содержат одинаковое число элементов. Это число является минимальным, с помощью которого можно реализовать заданную функцию в рассматриваемом элементном базисе.

§ 9.4. ОСНОВЫ СИНТЕЗА ЛИНЕЙНЫХ ПАССИВНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ

Задача синтеза четырехполюсников

Методы синтеза четырехполюсников менее разработаны, чем методы синтеза двухполюсников, однако в настоящее время эта область теории цепей интенсивно развивается. Синтез четырехполюсников, как и двухполюсников, можно производить во временной и частотной областях.

Рассмотрим методы синтеза в частотной области (т.е. по заданным операторным входным и передаточным характеристикам), отметив, что поскольку проходной четырехполюсник может быть представлен различными входными и передаточными характеристиками, возможны различные варианты постановки задачи синтеза. Например, синтез четырехполюсника по заданным выражениям для первичных или вторичных параметров; по заданной передаточной характеристике в режиме холостого хода на выходе; по заданной передаточной характеристике при согласованной чисто резистивной или произвольной нагрузке.

Критерии физической реализуемости четырехполюсников формулируются различным образом в зависимости от постановки задачи синтеза и заданного или выбранного элементного базиса. В общем случае на вид операторных передаточных характеристик линейной пассивной цепи Н (р) = N(p)lM (р) накладывается меньше органичений, чем на вид операторных входн1?1х характеристик. В частности, степени полиномов N (р) и М {р) могут отличаться больше чем на единицу, вещественная часть передаточ1ых функций на мнимой оси может быть отри-

1ателы10Й, а нули передаточных функций могут располагаться как в певой, так и в правой полуплоскостях (полюсы передаточных характеристик совпадают с нулями операторного входного сопротивления или эператорной входной проводимости и не могут располагаться в правой юлу плоскости).

Минимально-фазовые и неминимально-фазовые четырехполюсники

Рассмотрим два четырехполюсника А и Б, операторные коэффициенты передачи которых по напряжению определяются выражениями

к а (р) ={р + а)1{р + ь), Кб (р) = {р-а)/{р + Ь),

(9.9) (9.10)

где а, b - действительные положительные числа. Функции Кк (р) и Кб (р) имеют одинаковые полюсы /?ха =- Рхб = -Ь, расположенные в левой полуплоскости, и равные по модулю нули IpqaI = \Роб\ - = а, причем нуль функции Ха (р) лежит в левой (рис. 9.15, а), а нуль функции Кб (р) в правой (рис. 9.15, б) полуплоскости.

b+Ja>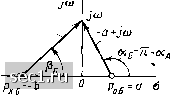

Рис. 9,15. К понятиям минимально-фазового и неминимально-фазового четырехполюсников

Заменяя в выражениях (9.9), (9.10) комплексную частоту р на ©, определим комплексные коэффициенты передачи рассматриваемых [етырехполюсников по напряжению

К а (/(й) - {а + /сй)/(й + /м); Кв (/W) = (-а + }(о)/{Ь + /ю).

(9.11) (9.12)

Каждый из двучленов, стоящих в числителе и знаменателе выражений (9.11), (9.12), можно изобразить на плоскости комплексного 1еременного р в виде вектора, проведенного из нуля или полюса функций К а (р), Кб (р) в произвольную точку /м, лежащую на мнимой эси (рис. 9.15). Следовательно, модули комплексных коэффициентов 1ередачи четырехполюсников по напряжению равны отношению длин