векторов, проведенных из нулей, к длинам векторов, проведенных из полюсов соответствующих функций:

К А (со) = J/V + M iVW+a (9.13)

Кб{о)УТ/УЩ (9.14)

а аргументы комплексных коэффициентов передачи четырехполюсников - разности углов, образуемых с положительным направлением вещественной оси векторами, проведенными из нулей, и векторами, проведенными из полюсов функций Ка {р) и Къ (р)-

ipA = «а - Ра = arctg (ю/а) - arctg (w/ft); (9.15)

фБ = «Б - Рб = л - arctg (w/a) - arctg (wfb). (9.16)

Как видно из выражений (9.13)-(9.16), модули комплексных коэффициентов передачи по напряжению обоих четырехполюсников равны, а аргумент комплексного коэффициента передачи по напряжению четырехполюсника А меньше, чем соответствующий аргумент четырехполюсника Б. Таким образом, при одинаковых модулях аргумент передаточной функции, имеющей нули в правой полуплоскости, больше аргумента передаточной функции, нули которой расположены только в левой полуплоскости. Полученный результат имеет весьма общий характер и распространяется па любые передаточные функции, имеющие произвольное число нулей и полюсов, расположенных не только на вещественной оси, но и в произвольных точках плоскости р.

В соответствии с указанным свойством четырехполюсники, передаточные функции которых не имеют нулей в правой полуплоскости, называются минимально-фазовыми, а четырехполюсники, у которых хотя бы один нуль расположен в правой полуплоскости, - неминимально-фазовыми.

комплексные частотные характеристики неминимально-фазовых четырехполюсников обладают рядом интересных особенностей. В частности, если у рассмотренного неминимально-фазового четырехполюсника Б параметры элементов выбраны таким образом, что

\р,ь\ = Кб! - а- ft, (9.17)

то его модуль коэффициента передачи по напряжению не зависит от частоты: /(б (со) - 1, а аргумент коэффициента передачи по напряжению с изменением частоты изменяется в пределах от я до 0: ijb (со) = я - 2arctg (со/а).

Четырехполюсник с АЧХ и ФЧХ такого типа называется фазовым контуром, все пропускающим четырехполюсником, или четырехполюсником чисто фазового сдвига. Фазовые контуры широко используют для коррекции ФЧХ цепей, т. е. когда необходимо изменить ФЧХ цепи без изменения ее АЧХ.

Пример 9.10. Определим операторный коэффициент передачи по напряжению симметричного мостового реактивного четырехполюсника (рис. 9.16) при согласованной нагрузке. Убедимся, что рассматриваемый четырехполюсник относится к фазовым контурам.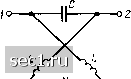

Используя выражения для первичных параметров симметричного мостового четырехполюсника (см. пример 8.14), определяем А-параметры:

. , , 2 Рис. 9.16. К примеру 9.10

pL-l/(pC) •

Характеристическое сопротивление такого четырехполюсника имеет чисто резистивный характер Zq (р) ~- А (Р)! (р) = T/L/C, а операторный коэффициент передачи по напряжению при согласованной нагрузке

УЛи (Р) -42 (Р) -f у ,2 (Р) Лг (Р) Р+ 1/VlC

Полюсы и нули (р) удовлетворяют условию (9.17), поэтому рассматриваемый четырехполюсник относится к фазовым контурам.

Существенное различие между минимально-фазовыми и неминимально-фазовыми четырехполюсниками заключается в том, что модуль и аргумент, равно как и вещественная и мнимая части, передаточной функции минимально-фазового четырехполюсника связаны однозначными зависимостями, которые отсутствуют у неминимально-фазовых четырехполюсников.

Методы реализации пассивных четырехполюсников

Задача синтеза четырехполюсников решается в два этапа: на первом этапе проверяют условия физической реализуемости заданных характеристик, на втором - определяют схему искомой цепи и параметры входящих в нее элементов. Оставляя открытым вопрос о физической реализуемости операторных передаточных характеристик, рассмотрим некоторые простые методы, позволяющие свести задачу реализации пассивных четырехполюсников к рассмотренной ранее задаче реализации пассивных двухполюсников.

Если синтез пассивного четырехполюсника производится по заданным выражениям для первичных или вторичных параметров, то эффективный способ решения задачи заключается в использовании П-образной или Т-образной канонических схем замещения взаимного четырехполюсника, приведенных на рис. 8.14, б, в. Операторные входные сопротивления или операторные входные проводимости пассивных двухполюсников, входящих в канонические схемы замещения, определяют с помощью соотношений (8.58), (8.59) по известным выражениям для Z- или К-параметров. Таким образом, задача синтеза пассивного четырехполюсника сводится к задаче синтеза пассивных двухполюсников, входящих в канонические схемы замещения.

• ••••

Пример 9.11. Найдем одну из возможных схем реализаций четырехполюсника, Y-параметры которого определяются выражениями

Y 720.10->8 p5,j-276.10-30 р8+ 12. IQ-i р

360-10-36 р« + 42-10->8р2+1

60-10-30 p3.L8.10-2 р

УгАР) = УЛР)=---- .См;

30.10- р2+1

270.10"3р34-30-10" Р--4-15-10" р-1 1 „

= 30.10-р+1 •

Выберем для реализации П-образную схему замещения четырехполюсника (см. рис. 8.14, в) и, используя соотношения (8.59), определим операторные входные проводимости входящих в нее двухполюсников:

4•10~p р

Yi (Р) = Уп (Р) + У,2 (Р) =----•

12-10-V-fl 3.10-[Р+1/(12.10-*)]

60.10-" рЗ + 8.10-2р „ ,

У2 (Р)--Уг. (Р) =-7?-- --2-10-2 р +

30-10-* р2+1

+ --- См

5-10-

30-10

- 18

Кз(р) = К22 (Р) + Г„(р) = 7.10-2 р+1. См.

Как видно из полученных выражений, двухполюсник Y (р) может быть реализован в виде последовательного соединения емкости С, = 4 пФ « индуктивности Li = 3 мкГн. Двухполюсник Y (р) реализуется в виде параллельного соединения емкости Сз = 2 пФ и последовательной LC-цепи, состоящей из емкости Cj = = 6 пФ и индуктивности = 5 мкГн, а двухполюсник Kg (р) - путем параллельного соединения сопротивления R = I Ом и емкости С4 = 7 пФ (рис. 9.17).

Синтезировать четырехполюсник по заданному операторному коэффициенту передачи по напряжению в режиме холостого хода 21х (.р) - N {р)/М (р) можно также с использованием П- или Т-образных канонических схем замещения. Для этого необходимо так подобрать выражения для его Y- или Z-параметров, чтобы они обеспечивали заданную передаточную характеристику

21х ip) = N (р)Ш ip) =- {р)1Уг ip) = {p)/Z,i (р)

и были физически реализуемы. Более просто реализовать заданный 21х (р) можно с помощью Г-образного четырехполюсника с Т-входом (см. рис. 8.17, а). Операторный коэффициент передачи по напряжению такого четырехполюсника в режиме холостого хода определяется выражением (8.122).

Для нахождения операторных входных сопротивлений двухполюсников, образующих продольную и поперечную ветви Г-образного четырехполюсника, приведем выражение для коэффициента передачи к виду (8.122). Это достигается путем деления полиномов N (р) и М (р) на некоторый полином Q (р):

К (р\ (Р) - •(P)/Q(P) - N(p)lQ (р)

М(р) M{p)iQ{p) N{p)iQ{p) + [M(p)-Nip)]/Q{p)