\У2(Р)

I

Рис. 9.17. К примеру 9.11

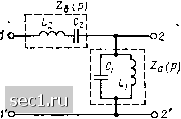Рис. 9.18 К примеру 9.12

выбранный таким образом, чтобы функции

Za (Р) - N ip)/Q (р) и Z, (р) = Ш (р) - N {p)VQ (р)

были физически реализуемыми.

Следует иметь в виду, что нули операторного коэффициента передачи по напряжению четырехполюсника, составленного по Г-образной схеме, совпадают с нулями сопротивления (р) и полюсами сопротивления Zj, (р) и, следовательно, находятся в левой полуплоскости. Поэтому Г-образную схему можно использовать только для реализации операторных передаточных характеристик минимально-фазовых четырехп олюсников.

Пример 9.12. Используя Г-образную схему, построим четырехполюсник, операторный коэффициент передачи по напряжению которого в режиме холостого хода

Cjix (Р) = 10р2/(180р + 37р2 -{ \)= N (р)1М (р).

Разделим числитель и знаменатель данного выражения на полином Q (р) - = ЗОр + 2р, выбранный таким образом, чтобы операторные входные сопротивления продольного (р) и поперечного Za (р) плеч Г-образного четырехполюсника представляли собой положительные вещественные функции:

Za (Р) =

Л (р)

Q(p) 15рН1 3(р2+1/15) Zb (Р) = [М (р) ~ N (p)]/Q (р) (12р2 4- 1)/(2р) - 6р

1/Г2р).

Как видно из полученных выражений, сопротивление Za (р) может быть реализовано в виде параллельного соединения емкости Ci= 3 Ф и индуктивности = 5 Гн, а сопротивление Zb (р) - в виде последовательного соединения индуктивности Lo - 6 Гн u емкости 2 Ф (рис. 9.18).

Четырехполюсник с заданным операторным коэффициентом передачи по напряжению в режиме холостого хода Kix (р) можно реализовать и по симметричной мостовой схеме (см. рис. 8.18, а), причем в этом случае нули Х21 х (/?) могут располагаться как в левой, так и в правой Полуплоскостях. Коэффициент передачи по напряжению полученного Четырехполюсника может быть выражен через сопротивления продольных Zl (р) и скрещивающихся (р) ветвей (см. пример 8.14):

Л21Х (р) = 221 (p)/Zii (р) = IZ, (р) - Zl {pMZip) + Zl (р)]. (9.18)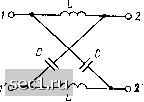

Рис. 9.19. К 9.13

Разделим числитель и знаменатель заданного выражения для K21X (р) на некоторый полином Q (р) и преобразуем полученное выражение к виду (9.18):

М(р) M(p)/Q(p) М (p) + N{p)]/Q (р)-[М (р)-УУ (p)]/Q (р) примеру m{p) + !(p)]!Q(p) + [M(p)~N(p)\/Q(p)

(9.19)

Из сравнения выражений (9.18) и (9.19) видно, что если полином Q (р) выбран таким образом, что операторные сопротивления

Zl (р) - Ш (р) - N {p)]/Q ip); Z, ip) = [М (p) -f N (p)l/Q (p) (9.20)

могут быть физически реализованы, то симметричный мостовой четырехполюсник, сопротивления продольных и скрещивающихся ветвей которого определяются выражениями (9.20), будет обладать заданным операторным коэффициентом передачи по напряжению.

Симметричный мостовой четырехполюсник можно использовать и для реализации заданного операторного коэффициента передачи по напряжению в режиме согласованной нагрузки. В этом случае К (р) и Zc (р) могут быть определены с помощью выражений (8.82), (8.86)*);

Zc (Р) = К Л12 (Р) Ми (р) = KZi(p)Z2(p);

К{р)=-

УЛ„ (р) (р) + УЛ12 (р) (р)

Используя (9.21), выразим сопротивления продольных и скрещивающихся ветвей четырехполюсника через сопротивление нагрузки Z„ (р) = Zc ip) и коэффициент передачи по напряжению:

Z, (р)= [l-.(p)]Z„ (р)/[1 +/С(р)];

Z2 (р) [1 + Л {р)\ Zh (р)/[1 - /С (р)1. (9.22)

Пример 9.13. Построим четырехполюсник, операторный коэффициент передачи по напряжению которого при согласованной нагрузке Z„ (р) = 10 Ом определяется выражением

К (р) - -(р - miip + щ.

Подставляя заданные К (р) и 2д (р) в выражения (9.22), определяем операторные сопротивления продольных (р) и скрещивающихся (р) ветвей симметричного мостового четырехполюсника:

Zl (р) = 10 • 10-6 р. Ом; Zj (р) = 1/(0,1 • 10-" р), Ом.

Таким образом, заданный коэффициент передачи может быть реализован с помощью реактивного мостового четырехполюсника (рис. 9.19)., содержащего индуктивности L = 10 мкГн в продольных и емкости С = 0,1 мкФ в скрещивающихся ветвях.

*) Выражение для Л-параметров симметричного мостового четырехполюсника приведены в примере 8.16.

Цепи

с распределенными параметрами

§ 10.1. ЗАДАЧА АНАЛИЗА ЦЕПЕЙ

С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Вводные замечания

Напомним, что цепями с распределенными параметрами называются идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных. Токи и напряжения в одномерной цепи с распределенными параметрами являются функциями двух переменных - времени t и координаты X.

Исторически сложилось так, что первыми в качестве одномерных цепей с распределенными параметрами стали представлять так называемые длинные линии, т.е. линии передачи энергии от источника к нагрузке, длина которых значительно превышает длину волны передаваемых электромагнитных колебаний. Поэтому одномерные цепи с распределенными параметрами часто называют длинными линиями или линиями,а уравнения (1.59), (1.60), описывающие зависимости между токами и напряжениями элементарного участка одномерной цепи с распределенными параметрами, - д и ф ф е-ренциальными.уравнениями длинной линии или телеграфными у.р авнениями. Будем использоват!? термины «длинная линия» или «линия» как синонимы термина «одномерная цепь с распределенными параметрами», помня при этом, что приведенная на рис. 1.41 схема элементарного участка одномерной цепи с распределенными параметрами и соответствующая ей система уравнений электрического равновесия (1.59), (1.60) носят общий характер и могут быть использованы не только для моделирования процессов в реальных линиях передачи, но и для приближенного представления многих других радиотехнических элементов и устройств в области достаточно высоких частот.

Одномерные цепи с распределенными параметрами, применяемые для моделирования различных реальных цепей и их элементов, отличаются одна от другой, в основном, значениями погонных параметров Ri, Li, С,, Gj и характером их зависимости от координаты, времени