будем называть коэффициентом распространения волновым сопротивлением линии. Представим коэффициент распространения линии в алгебраической

7 = а + /р, (10.14)

а волновое сопротивление линии и постоянные интегрирования в показательной

Л = Ai е*;

формах и преобразуем каждое из входящих в выражения (10.10), (10.11) слагаемых в показательную форму:

й {х) = {Ai е-« е-/(ЗА:-Ч.) +(2 е«) е/(Р+*);

/ (л:) = Л е-"* e-ZCP-+iO/zb -Л е»* e/(f*+*»-4»/zb.

Переходя от комплексных действующих значений напряжения и тока к мгновенным, получаем

и{х, 0 = 2 Л1е-"С05((й-рл:Н-ф1) + У2 Лае»* x

X со5{Ш + х + -; (10.15)

i(x, 0==-*--cos(w-PA; + ti-ф)---2- x

x C0s(ft) + par + »p2 -ф). (10.16)

Как видно из выражений (10.15), (10.16), установившиеся значения напряжения и тока в произвольном сечении линии, находящейся под гармоническим внешним воздействием, можно представить в виде суммы двух подобных по структуре, но отличающихся знаками перед коэффициентами аир составляющих:

и{Х, 0 = ипад(, 0+«отр(, 0; (10-17)

Цх, 0 = W(-*. 0 + отр( t). (10.18)

«пад (. о = К2 Аг е-« cos {Ш-х + ip); "отр (х, t)=Y2A е« cos («г- + 4- г!?); 1/2 i4 е~"*

W {х, t) = -2-!-COS (ш-pA;-f ф);

»отр . О =--COS ((Ot + х + 2-~Ч>)

1/2 у4 р«

L£j:kl cos (ю-f рл: + г32-Ф + Я).

При фиксированном х каждая из составляющих тока и напряжен,1я эедставляет собой гармоническую функцию времени t. В связи с м что сумма двух гармонических функций времени, имеющих одина-звую частоту, есть гармоническая функция времени той же частоты, шряжение и ток во всех сечениях линии изменяются по гармоничес-)му закону с частотой внешнего воздействия со (рис. 10.2). Как видно из рис. 10.2, а, для каждого фиксированного момента времени напряжение Мпад (х, t) изменяется вдоль линии по косинусоидально-му закону, причем амплитуда напряжения экспоненциально уменьшается с ростом X. При увеличении

Сточки функции Ыпад [х, t), ИМСЮ-

щие одинаковую фазу, смещаются вправо. Аналогичный вид имеют зависимости 1пад [х, t). Следовательно, и„ад {Х, t) представляют собой волны напряжения и тока, распространяющиеся в направлении увеличения х. Эти волны называют падающими или прямыми.

Из рассмотрения зависимостей "отр [х, f) и joTp [х, t) следует, что "отр (х, t) и ioTp (х, f) представляют собой волны напряжения и тока, распространяющиеся в направлении уменьшения х, т. е. от конца линии к ее началу (рис. 10.2, б). Эти волны называются отраженными или обратными.

Как видно из выражений (10.17), (10.18) и рис. 10.2, амплитуды на-яжения и тока падающей и отраженной волны уменьшаются в на-звлении распространения волн. Величина а, характеризующая гньшение амплитуды (действующего значения) падающей или отра-нной волны на единицу длины линии

(10.19)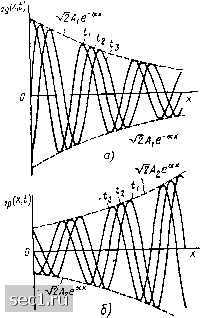

10.2. Распределение иапряженпя [ающей (а) и отраженной (б) волн

вдоль линии (/з>2>)

а = Re V = Re\Y{Ri + /wLi) (G + /(oCi) ],

зывается коэффициентом ослабления. Убывание плитуды волны связано с потерями энергии, поэтому для линии без герь (1 = Gi = 0) коэффициент ослабления а равен нулю, а ко; :})ициент распространения является чисто мнимым: у = /© YLiCi-Амплитуды падающей и отраженной волн напряжения и тока в ниях без потерь не зависят от координаты х и не изменяются вдоль

НИИ.

Мнимая часть комплексного коэффициента передачи линии р = = Im hl = Im iViRi + /«Li) (Gl + /coCi)!, характеризующая изменение фазы прямой или обратной волн на единицу длины линии, называется коэффициентом фазы. Для линии без потерь коэффициент фазы прямо пропорционален частоте

PcoKlTCi. (10.20)

Расстояние между двумя точками волны, фазы которых различаются на 2л, называется длиной волны. Длина волны в линии X определяется значением коэффициента фазы. Действительно, изменение фазы падающей или отраженной волны на участке линии длиной X

{iot -х + -[at-{x + %)+ = 2л,

откуда

X = 2я/р. (10.21)

Для линии без потерь X =- 2л/((й j/LiCi) = 1/(/KL,Ci).

Скорость перемещения вдоль линии точки волны, фаза колебания в которой остается неизменной, называется фазовой скоростью волны. Для падающей волны условие постоянства фазы записывается в виде

(wif-рд;+11)1) = const, или - (ю -pAr+ipi) =0,

откуда

"Ф.пад = dxidt = (й/р. (10.22)

Аналогичным образом находим фазовую скорость отраженной волны

Ф.отр -»/Р- (10.23)

Знак минус в выражении (10.23) указывает на то, что отраженная волна перемещается в направлении уменьшения х. Для линии без потерь фазовая скорость падающей и отраженной волн не зависит от частоты

=ф.пад = ф.отр = l/KlCi. (10.24)

Используя (10.21) и (10.22), получаем соотношения между фазовой скоростью и длиной волны в линии

X = 2лУф/а = Цф = ТОф. (10.25)

Из выражения (10.25) видно, что за время равное периоду внешнего воздействия Т, падающая и отраженная волны перемечаются на расстояние, равное длине волны X.

Итак, установлено, что напряжение и ток в любом сечении линии Можно рассматривать как результат наложения двух волн - падающей и отраженной. Зная это, нетрудно прийти к заключению, что первое и второе слагаемые, входящие в выражения (10.10), (10.11), представ-