Обозначая комплексные действующие значения этих величин через

= и {1)= и {х)\1 и = 1 (1) = i {x)\i = /2 и пола-

рая в (10.10), (10.11) X = I, получаем

U = Aie~-! е ; П = е- /Zb-А е /Zb,

откуда

JUb,j. 2hzblL-t . (10.37)

Подставляя (10.37) в (10.30), выражаем коэффициент отражения через ток и напряжение в конце линии:

р(;с) = AlI е-«--) =р,е-1. (10.38)

Здесь х = I - л: - расстояние, отсчитываемое от конца линии;

£2 = 9 {х)\.=1 = f/oTp (х)/[/пад (А:)и=г = (t/2 - Zbh)l{U2 + ад) -коэффициент отражения в конце линии, значение которого определяется только соотношением между сопротивлением нагрузки

Zh = UJti и волновым сопротивлением линии Zb:

P2 = (2„-Zb)/(Z„ + Zb). (10.39)

Как и всякое комплексное число, коэффициент отражения линии может быть представлен в показательной форме:

p(x) = p(x)e*pw.

Анализируя выражения (10.32), (10.38), устанавливаем, что модуль коэффициента отражения

Р W = foTp (х) = Pi е2« = Р2 е- 2«* (10.40)

плавно увеличивается с ростом х и достигает наибольшего значения

Ртах {Х) = Рг В конце линии.

Выражая коэффициент отражения в начале линии pi через коэффициент отражения в конце линии ра

Pi = p()U=o=P2e-- =р2е-2(а+/Р), (10.41)

находим, что модуль коэффициента отражения в начале линии в е" раз меньше, чем модуль отражения в ее конце. Из выражений (10.40), (10.41) следует, что модуль коэффициента отражения однородной линии без потерь имеет одно и то же значение во всех сечениях линии.

15 Зак. 565 449

с помощью формул (10.37), (10.39) напряжение и ток в произволь-ном сечении линии можно выразить через напряжение или ток и коэф. фициент отражения в конце линии:

ух -ух ух , -ух

о(.) 0 - - Zb (10.42)

ух -ух ух -ух

Выражения (10.42), (10.43) позволяют рассмотреть распределение напряжений и токов в однородной длинной линии в некоторых характерных режимах ее работы.

Режим бегущих волн

Режимом бегущих волн называется режим работы однородной линии, при котором в ней распространяется только падающая волна напряжения и тока, т.е. амплитуды напряжения и тока отраженной волны во всех сечениях линии равны нулю. Очевидно, что в режиме бегущих волн коэффициент отражения линии р (х) = 0. Из выражения (10.38) следует, что коэффициент отражения р (х) может быть равен нулю либо в линии бесконечной длины (при / = оо падающая волна не может достичь конца линии и отразиться от него), либо в линии конечной длины, сопротивление нагрузки которой выбрано таким образом, что коэффициент отражения в конце линии pg = == 0. Из этих случаев практический интерес представляет только второй, для реализации которого, как видно из (10.39), необходимо, чтобы сопротивление нагрузки линии было равно волновому сопротивлению Zb (такая нагрузка называется согласованной).

Полагая в выражениях (10.35), (10.36), (10.42), (10.43) р2 = Pi = = О, выразим комплексные действующие значения напряжения и тока в произвольном сечении линии через комплексные действующие значения напряжения и тока /i в начале или в конце линии (О2, 2)-f) (X) = {У„,д (х) = f/ е= t/i е-51

/W = /пaдW=/eI=Ae- Представим напряжение и ток в начале линии в показательной форме: t/i = /le*", /1= /1 е* и перейдем от комплексных дейст вующих значений напряжения и тока к мгновенным:

и (х, t) = Y2 Ul е--"cos (Ы-х + ip„i);

f (X,/)=y2/ie-«cos(u) -px + ila). (10.44)

Как видно из выражений (10.44), в режиме бегущих воли амплитуды напряжения и тока в линии с потерями (а > 0) экспоненциально убывают с ростом х, а в линии без потерь (а = 0) сохраняют одно и то же значение во всех сечениях линии (рис. 10.3).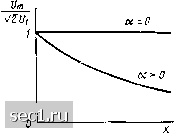

Рис. 10.3. Распределение амплитуд напряжения вдоль линии в режиме бегущих волн

Начальные фазы напряжения -

рлг и тока урн - рл: в режиме бегущих волн изменяются вдоль линии по лилейному закону, причем сдвиг фаз между напряжением и током во всех сечениях линии имеет одно и то же значение f„i - ila-

Входное сопротивление линии в ре-я<име бегущих волн равно волновому сопротивлению линии и не зависит от ее длины:

Z„(/co)=(;i i = [;(x) (jc) =

= >„ад() падН=2в.

У линии без потерь волновое сопротивление имеет чисто резистивный ха-рактер (10.28), поэтому в режиме бегущих волн сдвиг фаз между напряжением н током во всех сечениях лиини без потерь равен нулю.

Мгновенная мощность, потребляемая участком линии без потерь, расположенным правее произвольного сечения х (см. рис. 10.1), равна произведению мгновенных значений напряжения и тока в сечении х:

р {х, t) = и (х, t) i {х, t) = 2UiU cos- - pjc - ijii). (10.45)

Из выражения (10.45) следует, что мгновенная мощность, потребляемая произвольным участком линии без потерь в режиме бегущих волн, не может быть отрицательной, следовательно, в режиме бегущих волн передача энергии в линии производится только в одном напрсп-лении - от источника энергии к нагрузке.

Обмен энергией между источником и нагрузкой в режиме бегущих волн отсутствует и вся энергия, передаваемая падающей волной, потребляется нагрузкой.

Режим стоячих волн

Если сопротивление нагрузки рассматриваемой линии не равно волновому сопротивлению, то только часть энергии, передаваемой падающей волной к концу линии, потребляется нагрузкой. Оставшаяся часть энергии отражается от нагрузки и в виде отраженной волны возвращается к источнику. Если модуль коэффициента отражения линии р (х) == 1, т.е. амплитуды отраженной и падающей волн во всех сечениях линии одинаковы, то в линии устанавливается специфический режим называемый режимом стоячих волн. Согласно выражению (10.40) модуль коэффициента отражения р (х) = 1 только тогда, когда модуль коэффициента отражения в конце линии = 1, а коэффициент ослабления линии а = 0. Анализируя выражение (10.39), можно убедиться, что рз = 1 только в трех случаях: когда Сопротивление нагрузки равно либо нулю, либо бесконечности, либо Имеет чисто реактивный характер.