столбец напряжений ветвей и, получаем

В X и =

21 23

...Ь

«2

21 «1 + «2 Ч •• • + 2Р "р

ЬщЬпг--- Ьп1> JL"pJ l.nl «1 + Ьп2 «2 4-...+bnp«p

Каждая строка этого выражения представляет собой алгебраическую сумму напряжений ветвей, входящих в i-й главный контур, причем правило суммирования напряжений ветвей совпадает с соответствующим правилом, установленным для записи уравнений баланса напряжений в контуре (1.40). Так как в соответствии со вторым законом Кирхгофа сумма напряжений ветвей, входящих в каждый контур, в любой момент времени равна нулю, то окончательно имеем

В X U = 0.

(1.52)

Выражение (1.52) является матричной формой записи уравнений баланса напряжений для главных контуров цепи. Уравнения, входящие в (1.52), являются линейно независимыми, так как каждое из них отличается от остальных, по крайней мере, одним напряжением - напряжением главной ветви, замыкающей данный контур.

Таким образом, система изп=-р - q+l главных контуров, со-отвежтвующих выбранному дереву, является системой независимых контуров. Следовательно, для каждой цепи можно составить п независимых уравнений по второму закону Кирхгофа.

Пример 1.5. Рассмотрим применение матрицы контуров для формирования системы линейно независимых уравнений баланса напряясений для цепи, граф которой приведен на рис. 1.26. Умножая матрицу главных контуров этой цепи (1.51) на матрицу-столбец напряжений ветвей и, получаем

В X и-

10 0 1110

0 10 1110

0 0 1 -10 0 0

ООО 0101

"а

«3 "4

"г, «в

(1.53)

Следует отметить, что при выборе системы независимых контуров было использовано достаточное условие независимости уравнений, заключающееся в том, что для линейной независимости системы уравнений достаточно, чтобы каждое из уравнений содержало, по крайней море, одну независимую переменную величину, отсутствующую в других уравнениях. Так как это условие не является необходимым, то для каждой цепи можно найти и другие системы независимых контуров, которые в ряде случаев могут не совпадать ни с одной из систем главных контуров. В частности, ячейки плоского гряфа, число которых оказывастся равным п р - q \ 1, представляют собой систе-

му независимых контуров. Их состав может быть описан матрицей основных контуров Bp, которая строится аналогично матрице главных контуров (контуры, соответствующие каждой из ячеек, нумеруют от 1 до п, каждому из них приписывают произвольную ориентацию). Например, для графа электрической цепи, изображенного на рис. 1.35:

В» =

• номера ветвей

(1.54)

2 3 4 t

номера контуров

В этом случае матрица основных контуров не совпадает ни с одной из возможных для данного графа матриц главных контуров.

Матрицу В° можно, как и матрицу В, использовать для записи системы линейно независимых уравнений баланса напряжений:

В» X U = 0.

(1.55)

Так, используя (1.54), можно составить систему уравнений баланса напряжений для ячеек графа, изображенного на рис. 1.35:

В° X и =

о о о

"1

«8 «4

«5 «в

"7

Следует подчеркнуть, что понятие ячейки (окна) было введено ранее только для плоских графов и что только для них возможен выбор ячеек в качестве независимых контуров.

Дуальные графы и дуальные цепи

Два плоских графа называются дуальными, если матрица узлов одного из них А равна матрице основных контуров В° другого и наоборот:

Ai = В°; Аа = Щ. (1.56)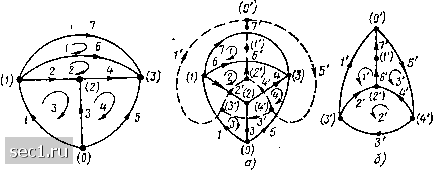

Рис. 1.35. К составлению основной матрицы контуров

Рис. 1.36. Построение дуального графа (заданный граф - сплошные линии)

Очевидно, что дуальные графы должны иметь одинаковое число ветвей (pi = Р2), причем число ветвей дерева одного из них т должно быть равно числу главных ветвей п другого:

Для построения графа, дуального заданному (рис. 1.36, а), необходимо внутри каждой ячейки исходного графа разместить узел дуального графа [{!), (2) и т. д.], кроме того, один узел дуального графа pacпoлaaeтcя во внешней по отношению к исходному графу части плоскости, т. е. в базисной ячейке. Узлы дуального графа соединяются между собой ветвями так, чтобы каждая ветвь исходного графа пересекала одну ветвь дуального графа (пунктир на рис. 1.36, а). Номера узлов дуального графа совпадают с номерами контуров исходного графа, внутри которых они размещены. Узлу дуального графа, расположенному в базисной ячейке, присваивается номер О. Пересекающимся между собой ветвями исходного и дуального графов присваиваются одинаковые номера. Ориентация ветвей и контуров дуального графа (рис. 1.36, б) выбирается таким образом, чтобы обеспечить выполнение равенств (1.56).

Нетрудно убедиться, что матрицы узлов Ag и основных контуров В° дуального графа (рис. 1.36,6) равны соответственно матрицам основных контуров BJ и узлов Ai исходного графа:

А, = В? =