Аналогичными свойствами обладает отрезок линии без потерь длиной 3V8.

Трансформирующие свойства отрезков длинных линий широко используются на практике для построения устройств согласования реальных линий передачи с нагрузкой. В результате согласования в линии передачи устанавливается режим, близкий к режиму бегущих волн, при этом практически вся передаваемая линией энергия потребляется нагрузкой, а потери энергии, связанные с многократным прохождением отраженных волн

...J-l

во вт И" во "ВТ ~Л-,,2 rl-(

вдоль линии значительно уменьшаются.

Если сопротивление нагрузки реальной линии передачи с малыми потерями имеет чисто резистивный характер, то для согласования линии с нагрузкой можно применять четвертьволновый трансформатор, включенный между линией и нагрузкой (рис. 10.11, а). Погонные параметры отрезка линии, используемой в качестве четвертьволнового трансформатора, выбирают таким образом, чтобы волновое сопротивление трансформатора 7?вт было равно среднему геометрическому из волнового сопротивления основной (согласуемой) линии Rbo и сопротивления нагрузки /?„:

Рис. 10.11. Согласование линии с нагрузкой с помощью четвертьволнового трансформатора

В этом случае входное сопротивление четвертьволнового трансфо]-матора в точках 1-/ равно Rbo, и в основной линии установится режим, близкий к режиму бегущих волн. Отрезок линии, используемый в качестве четвертьволнового трансформатора, при этом находится в режиме смешанных волн, однако вследствие малой длины трансформатора потери энергии в нем незначительны.

Если сопротивление нагрузки линии имеет комплексный характер, то согласующий трансформатор подключают не в непосредственной близости к нагрузке, а на некотором расстоянии Iq от нее, выбранном таким образом, чтобы входное сопротивление нагруженного участка линии в точках 2-2 имело чисто резистивный характер (рис. 10.11, б). Неудобство рассмотренного метода согласования заключается в том, что необходимо изготавливать специальный отрезок линии, волновое сопротивление и, следовательно, погонные параметры которого должны отличаться от волнового сопротивления и погонных параметров согласуемой линии.

Этого недостатка лишен разработанный В. Р. Татариновым метод согласования с помощью одного или двух реактивных шлейфов, конструктивно представляющих собой отрезки длинных линий того же типа, что и согласуемая линия (рис. 10.12). В первом случае расстояние от места подключения шлейфа до точки подключения нагрузки /о

I рис.

10.12, a) выбирают таким

образом, чтобы вещественная составляющая входной проводимости линии в точках /-/ была равна \Rb-

1 Ra t jb, (10.71)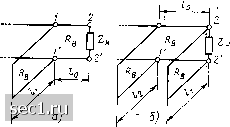

PiK- 10.12. Согласование линии с на-ipvsKoii с помощью одного (а) нли дну\ (6) реактивных шлейфов

а длину шлейфа /, ~ так, чтобы входная проводимость шлейфа равнялась - jb. Очевидно, что при этих условиях эквивалентное сопротивление нагрузки

основной линии в точках /-Г равно волновому сопротивлению линии Rb-

Во втором случае (рис. 10.12, б) расстояние между шлейфами /„ выбирают равным к/8 или -Зк-8, длина первого шлейфа /i подбирается так, чтобы в точках 1-/ выполнялось условие (10.71), а длина второго шлейфа I., - так, чтобы компенсировать мнимую составляющую Кц-

Определение параметров однородной длинной линии по результатам опытов холостого хода и короткого замыкания

С помощью полученных соотношений можно определить волновые и погонные параметры однородной длинной линии по результатам измерения комплексного входного сопротивления отрезка линии в режимах холостого хода и короткого замыкания на выходе. Разрешим (10.65), (10.67) относительно Zb и th {yl):

Zb~\ ZZ,\

(10.72)

th(7/) = l/Z,/Z,

\ Z,7,.

(10,73)

Из выражений (10.72), (10.73) видно, что волновое сопротивление линии равно среднему геометрическому из комплексных входных сопротивлений отрезка линии произвольной длины /, измеренных в режимах холостого хода и короткого замыкания на выходе, а гиперболический тангенс произведения коэффициента распространения линии на ее длину - среднему геометрическому из комплексного входного сопротивления отрезка линии в режиме короткого замыкания и комплексной входной проводимости этого же отрезка в режиме холостого хода.

Комплексное входное сопротивление любого отрезка длинной линии, нагруженного на произвольное сопротивление Z„, можно выразить через комплексные входные сопротивления этого отрезка, изме-

.1 к ЪьЬ

репные в режимах холостого хода и короткого замыкания. Действц 1ельно, подставляя (10.72), (10,73) в выражение (10.64), получаем

Z i!LlbZBcth(,/)-i!i±lz..

Для определения коэффициента ослабления а и коэффициента фазы линии р перейдем в (10.73) от гиперболического тангенса к показательным функциям

th(Y0-(e--e--)(e-4e-t)-(e-l)/(e1 -

и разрешим полученное выражение относительно е - :

e =(l-fT Z3)/(l-Vz;Tx) = e*. (10.74)

Используя (10.74), выражаем а и р через модуль А и аргумент ф комплексного числа (1 -f Vz„yx)(l - уУ х)-

а ]пЛ/(2/); р , \ 2kn) {21).

Здесь k - коэффициент, равный целому числу длин волн, укладывающихся вдоль длины исследуемого отрезка.

По результатам измерения 7 и Zb можно определить погонные параметры линии Rl, Li, Ci, Gy. Разрешая выражения (10.12), (10.13) относительно Rl J jwLi и Gj т ycoCi и приравнивая вещественные и мнимые части получаемых равенств: i /wL, ZbY, Gj - /wCj

y/Zfl, находим

i-Re[ZBXl; mLi lm[ZBY]; Gi -ReY 2b1; coCi InMV/Bl-

§ 10.4. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Задачи анализа переходных процессов в цепях с распределенными параметрами

Различают два типа задач, связанных с исследованием переходных процессов в одномерных цепях с распределенными параметрами:

1) определение токов и напряжений на зажимах линии или в более общем случае токов и напряжений внешних по отношению к линии ветвей прн произвольном внешнем воздействии;

2) определение напряжений и токов в различных сечениях линии при произвольном внешнем воздействии.

Эти задачи обычно решают операторным методом. При решении задач первого типа операторные изображения искомых токов и напряжений находят с помощью рассмотренных ранее методов анализа сложных цепей, причем линию рассматривают как четырехполюсник, первичные параметры которого считаются известными. При реШни задач второго типа операторные нюбражения токов и напряжении различных сечених линии определяют из выражений (10.7), (О-