Как видно из рис. 1.36, ячейки дуального графа соответствуют узлам исходного графа, а узлы дуального графа - ячейкам исходного. Лоследовательному соединению ветвей исходного графа соответствует параллельное соединение ветвей дуального графа и наоборот. Если сформулированное правило нахождения дуального графа применить для построения графа, дуального изображенному на рис. 1.36, б, то получится граф, изоморфный исходному графу (рис. 1.36, а сплошные линии).

Используя понятие дуального графа, легко обобщить введенное ранее понятие дуальных цепей. Две цепи называются дуальными, если они имеют дуальные графы и каждому элементу одной цепи соот-

0) (2) r а)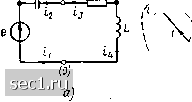

(О) 5)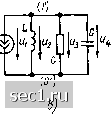

Рис. 1.37. К примеру 1 6

ветствует дуальный элемент другой. Для построения дуальной цепи сначала находят граф, дуальный расширенному топологическому графу исходной цепи, а затем каждую ветвь дуального графа заменяют элементом, дуальным элементу, расположенному в соответствующей ветви исходной цепи.

Пример 1.6. Построим, цепь, дуальную приведенной на рис. 1.37, а. На рис. 1.37, б сплошными линиями показан граф исходной цепи, а пунктирными - дуальный ему граф (направление ветвей исходного графа соответствует направлению токов ветвей исходной цепи, а направление ветвей дуального графа-• направлению напряжения ветвей дуальной цепи). Цепь, дуальная исходной, изображена на рис. 1.37, в.

Из определения дуальной цепи и равенств (1.56) следует, что уравнения баланса токов для одной из дуальных цепей будут совпадать с Уравнениями баланса напряжений для другой при условии, что в соответствующих уравнениях токи ветвей одной цепи будут заменены на напряжения ветвей другой цепи и наоборот. Это свойство дуальных цепей иногда используют в качестве определения дуальных цепей.

В заключение заметим, что непланарные графы не имеют дуальных графов, в связи с чем идеализированной электрической цепи, схема которой не является планарной, не может быть поставлена в соответствие дуальная цепь.

§ 1.5. УРАВНЕНИЯ ЭЛЕКТРИЧЕСКОГО РАВНОВЕСИЯ ЦЕПЕЙ

Рис. 1.38. Представление электрической цепи в виде системы с /V входами и М выходами

Основные задачи теории цепей

Любую электрическую цепь можно рассматривать как систему с одним или несколькими входами и одним или несколькими выходами (рис. 1.38). Если к входам цепи приложить внешнее воздействие X (t) = {xj (t), xit), Xn (t)}, TO на выходах можно обнаружить реакцию или отклик у (t) = {у (t), у (t), .... ум (t)}, тце N и М - число входов и выходов соответственно. В зависимости от исходных данных и конечной цели исследования в теории цепей различают две

группы задач: задачи анализа и задачи синтеза.

Задача анализа электрической цепи состоит в определении реакции цепи у (t) на заданное внешнее воздействие х (t).

Задача синтеза цепи заключается в нахождении цепи по заданной реакции цепи у (t) на некоторое внешнее воздействие х (t).

Исходными данными в задаче анализа являются эквивалентная схема цепи с параметрами всех входящих в нее элементов и описание внешнего воздействия х (t), задаваемого в виде совокупности токов и напряжений идеализированных неуправляемых источников. В результате анализа определяется отклик у (t) в виде совокупности токов и напряжений всех или некоторых ветвей цепи. В частном случае задача анализа может сводиться к определению соотношений между реакциями цепи на отдельных выходах yj (t) и воздействиями Xi (t), приложенными к определенным входам. Такие соотношения называются характеристиками (системными функциями, функциями) цепи. В зависимости оттого, какая величина-частота или время - является аргументом в выражениях, описывающих соотношения между откликом и внешним воздействием, различают частотные и временные характеристики цепи. Определение и исследование частотных характеристик представляют собой задачу анализа цепи в частотной области; нахождение временнйх характеристик -задачу анализа цепи во временной области.

Исходными данными в задаче синтеза являются описания внешнего воздействия х (t) и ее отклика у (i). В результате синтеза необходимо найти эквивалентную схему цепи и параметры всех входящих в нее элементов. В частном случае задача синтеза может сводиться к нахождению цепи, обеспечивающей заданные соотношения между внешним воздействием на цепь Xi {() и ее реакцией yj (t), т. е. к нахождению цепи по ее характеристикам.

Анализ и синтез электрических цепей в определенной степени взаимосвязаны, в частности методы синтеза базируются на использовании

общих свойств характеристик различных классов цепей, которые изучаются в процессе анализа. Поэтому изложению методов синтеза цепей будет предшествовать рассмотрение общих методов анализа цепей и знакомство с характеристиками некоторых классов цепей при различных внешних воздействиях.

Понятие об уравнениях электрического равновесия.

Математически задача анализа электрической цепи сводится к составлению и решению системы линейно независимых уравнений, в которых в качестве неизвестных фигурируют токи и напряжения ветвей исследуемой цепи. Уравнения, решение которых позволяет определить токи и напряжения ветвей электрической цепи, называются уравнениями электрического равновесия цепи. Очевидно, что число уравнений электрического равновесия должно быть равно количеству неизвестных токов и напряжений.

В общем случае в цепи, содержащей р ветвей и q узлов, имеется 2р неизвестных токов и напряжений ветвей. Используя законы Кирхгофа, для такой цепи можно составить т = q- 1 независимых уравнений баланса токов ап = р - q+ \ независимых уравнений баланса напряжений. В сочетании с компонентными уравнениями (уравнениями ветвей) получаем 2р линейно независимых уравнений, что достаточно для определения неизвестных токов и напряжений ветвей.

Если в рассматриваемой цепи и.меется р,,., ветвей, в которых содержатся идеализированные источники тока (токи этих ветвей заданы, а напряжения неизвестны), и ветвей, составленных только из идеализированных источников напряжения (напряжения этих ветвей известны), то общее число неизвестных токов и напряжений уменьшается до 2р - /?„т - /?ин- Для определения этих неизвестных нужно составить лишь 2р - рт - pan линейно независимых уравнений {т -\- п = р уравнений на основании законов Кирхгофа яр -ри,: -- /?ин компонентных уравнений для ветвей, не содержащих указанных источников).

Таким образом, используя компонентные уравнения и топологические уравнения, составленные на основании законов Кирхгофа, всегда можно сформировать систему уравнений электрического равновесия, число уравнений в которой достаточно для определения всех неизвестных токов и напряжений. Будем называть такую систему уравнений о с-новной системой уравнений электрического равновесия цепи.

На практике для анализа цепей используют различные методы составления уравнения электрического равновесия, в частности методы токов ветвей, напряжений ветвей, контурных токов, узловых напряжений, переменных состояния. Все они базируюжя на использовании различных приемов, позволяющих преобразовать основную систему уравнений электрического равновесия и уменьигить по сравнению с 2р или 2р - pat - Рт число одновременно решаемых уравнений.

Как было показано ранее, уравнения (1.37) и (1.40) являются алгебраическими, а компонентные уравнения идеализированных пассив-