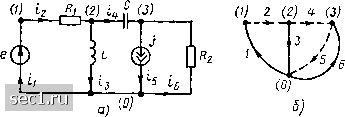Рис. 1.39. К примеру 1.7

ных элементов могут быть как алгебраическими (1.9), (1.10), так и дифференциальными (1.13), (1.22) или интегральными (1.16), (1.23). Вследствие этого уравнения электрического равновесия цепи, состивлен-ные любым методом, представляют собой в общем случае систему ин-тегродифференциальных уравнений.

• ••••

Пример 1.7. Составим основную систему уравнений электрического равновесия цепи, схема и топологический граф которой изображены на рис. 1.39, п и б соответственно. Для этой цепи р = 6, q = 4, рт 1 и рин - 1- Общее число неизвестных токов и напряокений ветвей 2р - р„т - Рин ~ Ю. Используя законы Кирхгофа, можно составить т q - I ~- уравнения баланса токов:

- 1г 4 «2 0; - «2 4 is 4 U - 0; f у - (, = О

и п =~ р - <?+1 - 3 уравнения баланса напряжений:

«2 4 "з ~= е (0; - «3 4- «4 - "а 0; - иь 4 «в 0.

Кро.ие того, имеем р - рит - Рин 4 уравнений ветвей, не содержащих идеализированных источников:

«4 ==«4 (0)4-

В результате получаем систему из 10 линейно независимых уравнений для

определения «Б, в, «е.

10 неизвестных токов и напряжений: ij, (j, Uj, (j

«4.

Система уравнений электрического равновесия цепи, составленная любым методом, может быть путем дифференцирования и последовательного исключения неизвестных сведена к одному дифференциальному уравнению для любого из неизвестных токов и напряжений, называемому дифференциальным уравнением цепи. В частном случае это может быть алгебраическое уравнение, которое можно рассматривать как дифференциальное уравнение нулевого порядка. Дифференциальное уравнение цепи содержит фундаментальную информацию о характере имеющих место в цепи электрических процессов и является основой для классификации электрических цепей.Тип дифференциального уравнения цепи полностью определяется ее топологией и характером входящих в нее идеализированных элементов.

Пример 1.8. Применяя указанные преобразования к основной системе уравнений электрического равновесия цепи (рис. 1.39, а), получим дифференциальное уравнение этой цепи, составленное относительно напряжения и:

аг fa + °t+Qo "з = /(О-

Здесь ао = 1/(LC); а, = (L + R.RC)!(RiCL); а = (R + R)/R-постоянные коэффициенты, определяемые пара.иетрами пассивных элемрнтов цепи;

f (t) - + lR7C~dr ~ ФучЦия времени, определяе-

мая параметрами независимых источников напряжения и тока.

Таким образом, уравнение цепи, изображенной на рис. 1.39, является линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами

Классификация электрических цепей

Электрические цепи, составленные из идеализированных элементов, могут быть классифицированы по ряду признаков:

по топологическим особенностям: планарные (плоские) и непланарные (объемные), разветвленные и неразветвлен-ные, простейшие (одноконтурные, двухузловые) и сложные (многоконтурные, многоузловые);

по энергетическим свойствам: активные (содержащие идеализированные активные элементы) и пассивные (не содержащие идеализированных активных элементов);

по числу внешних выводов: двухполюсники и многополюсники; и др.

Классификация цепей по этим признакам не носит принципиального характера и используется, в основном, с целью упорядочения терминологии.

Фундажнтальный характер имеет классификация цепей в зависимости от вида дифференциального уравнения цепи. Идеализированные электрические цепи, процессы в которых описываются обыкновенными дифференциальными уравнениями, называются цепями с сосредоточенными параметрами. Цепи такого типа используют в качестве упрощенных моделей реальных электрических цепей и их элементов на сравнительно низких частотах, когда длина волны электромагнитных колебаний существенно больше размеров исследуемого устройства. При этих условиях в исследуемых устройствах и их элементах удается выделить конечное число* участков, в которых преобладает какой-то один из основных эффектов - запасание энергии электрического или магнитного полей, преобразование электрической энергии в другие виды энергии или преобразование энергии сторонних сил в электрическую. Токн рассматриваемой реальной цепи, являясь функциями времени, имеют одинаковые мгновенные значения в пределах каждого из выделенных участков. Заменяя эти участки идеализированными активными или пассивными элементами, получают идеализированную цепь, содержащую конечное число элементов, значения параметров которых конечны.

Таким образом, цепи с сосредоточенными паражтрами представляют собой идеализированные цепи, моделирующие реальные устройства или их элементы при условиях, когда можно предположить, что каждый из основных электрических эффектов сосредоточен в конечном числе пространственно локализуемых областей.

Когда длина волны электромагнитных колебаний соизмерима с размерами исследуемого устройства или его элементов, пространственно локализовать области, в которых сосредоточены только эффекты одного типа, не удается. Это связано с тем, что даже при бесконечно малой длине выделяемых участков, в пределах каждого из них имеют место одновременно несколько из перечисленных основных эффектов, причем значения токов в пределах выделенных участков изменяются

от одного сечения к другому. При этих условиях цепи, моделирующие реальные устройства или их элементы, содержат бесконечно большое число идеализированных элементов, параметры которых имеют бесконечно малые значения. Рис. 1.40. Упрощенная коист- Процессы в таких цепях описываются рукция конденсатора: дифференциальными уравнениями в

обкладки, 2-диэлектрик частных производных. Идеализирован-

ные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных, называются цепями с распределенными параметрами.

Следует подчеркнуть, что термины щепь с распределенными параметрами-» и щепь с сосредоточенными параметрами» применимы только к идеализированным (моделирующим) цепям и не должны использоваться для характеристики реальных цепей.

В зависимости от условий и требуемой точности исследования каждый элемент реальной цепи и, следовательно, каждая реальная цепь в целом могут быть заменены моделирующей цепью с сосредоточенными или распределенными параметрами. Например, конденсатор любого типа конструктивно представляет собой две проводящие обкладки 7 и <3, разделенные слоем диэлектрика 2 (рис. 1.40). В области частот, когда длина волны электромагнитных колебаний значительно превышает геометрические размеры обкладок, он может быть представлен одной из моделирующих цепей с сосредоточенными параметрами, схемы которых приведены на рис. 1.11. На более высоких частотах, когда длина волны электромагнитных колебаний сравнима с геометрическими размерами обкладок, но существенно больше расстояния между ними, необходимо учитывать, что процессы запасания энергии электрического и магнитного полей, а также необратимое преобразование электрической энергии в другие виды энергии имеют место вдоль всей длины обкладок конденсатора. В этом случае эквивалентная схема элементарного участка конденсатора длиной dx состоит из индуктивности Lq и емкости Со, характеризующих процессы запасания энергии магнитного и электрического полей, а также сопротивления и проводимости утечки Go, учитывающих потери энергии в конденсаторе