(рис. 1.41, а). Эквивалентная схема всего конденсатора должна состоять из бесконечно большого числа таких секций. Следовательно, идеализированная цепь, моделирующая конденсатор в рассматриваемом диапазоне частот, представляет собой цепь с распределенными параметрами.

На примере цепи, эквивалентная схема которой изображена на рис. 1.41, а, покажем, что электрические процессы в цепях с распределенными параметрами описываются дифференциальными уравнениями в частных производных. Действительно, ток i = i {х, t) и на-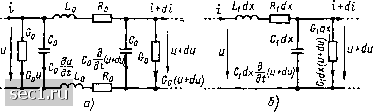

Рис. 1.41. Эквивалентные схемы элементарного участка конденсатора

(рнс 1.40)

пряжение и - и {х, t) рассматриваемой цепи являются функциями времени t и координаты х. Приращения тока и напряжения на участке цепи длиной dx

dl~- dx; du = dx.

dx dx

Полагая, что параметры элементов моделирующей цепи Ro, Lg, Со и G„ не зависят от токов и напряжений и выражая их через погонные (т. е. приходящиеся на единицу длины) параметры Ri, L, и

Ro - {Ri/2)dx; Lo - iU2)dx; C„ =- (C,/2)dx; Go = (Gi/2)dx,

составим уравнения баланса токов и напряжений элементарного участка цепи:

G, , 2

+ 2fdxJ[i-.fdxufdx).u+JL0.iL,S)

2 dt }

(1.57)

Пренебрегая величинами второго порядка малости, уравнение (1.57), (1.58) можно преобразовать к виду

Jl «.,-+i.JL. 0.60

Решая уравнения (1.59), (1.60) при соответствующих начальных i граничных условиях, можно определить токи и напряжения цепи моделирующей коденсатор в рассматриваемом режиме.

Отметим, что уравнениям (1.59), (1.60) может быть поставлена в соответствие более простая эквивалентная схема элементарного участка цепи (рис. 1.41, б). Аналогичный вид имеют высокочастотные схемы замещения и ряда других элементов, входящих в состав радиоэлектронных устройств, в частности двухпроводных и коаксиальных линий передачи.

В зависимости от числа координат, вдоль которых происходит изменение тока и напряжения и вдоль которых «распределены» параметры цепи, различают одномерные, двухмерные и трехмерные цепи с распределенными параметрами. В теории цепей рассматривают, в основном, одномерные цепи с распределенными параметрами, процессы в которых описываются дифференциальными уравнениями типа (1.59), (1.60).

Параметры рассмотренных ранее идеализированных линейных пассивных элементов не зависят от значений токов и напряжений соответствующих элементов и, следовательно, от интенсивности внепшего воздействия на цепь, определяемой токами действующих в цепи независимых источников тока и напряжениями действующих в цепи независимых источников напряжения. Связь между током и напряжением линейных идеализированных пассивных элементов описывается линейными алгебраическими, дифференциальными или интегральными уравнениями, иными словами, компонентные уравнения этих элементов являются линейными.

Параметры нелинейных пассивных элементов зависят от токов или напряжений соответствующих элементов, а следовательно, и от интенсивности внеппюго воздействия. Компонентные уравнения нелинейных идеализированных пассивных элементов - нелинейные.

В зависимости от вида компонентного уравнения идеализированные активные элементы также делятся на линейные и нелинейные. К линейным идеализированным активным элементам относят независимые i< линейно управляемые зависимые источники тока и напряжения, к нелинейным - нелинейно управляемые зависимые источники тока i напряжения.

Цепь с сосредоточенными или распределенными параметрами, составленная только из линейных и;1салпзнроваиных элементов, иазы ваегся л и п е и н о и. Дифференппальное уравнеши* такой цепи - линейное. Если в состав цспм входит хотя бы один иелииейиып пассив иый или активный элсмснг. то она называется н е л п и е й н о й , а

процессы в ней описываются нелинейными дифференциальными уравнениями.

Параметры линейных идеализированных пассивных элементов и коэффициенты управления линейно управляемых источников могут либо иметь постоянные значения, либо изменяться во времени под действием некоторых факторов, непосредственно не связанных с токами или напряжениями этих элементов (например, емкость конденсатора может изменяться во времени вследствие изменения расстояния между обкладками; индуктивность катушки можно изменять путем перемещения сердечника). Идеализированные элементы первого типа называют линейными элементами с постоянными параметрами, элементы второго типа - линейными элементами с переменными параметрами или параметрическими элементами. Параметрические элементы, у которых изменение параметров происходит с частотой, близкой к частоте токов или напряжений этих элементов, следует отличать от регулируемых элементов -конденсаторов переменной емкости, вариометров, подстроечных конденсаторов и др., у которых изменение параметров производится весьма медленно и только-в процессе настройки или регулировки соответствующего устройства. При составлении уравнений электрического равновесия параметрам регулируемых элементов приписывают некоторые фиксированные значения, а сами элементы относят к элементам с постоянными параметрами.

Цепи, составленные только из линейных элементов с постоянными параметрами, называются линейными цепями с постоянными параметрами или линейными инвариантными во времени цепями. Процессы в линейных инвариантных во времени цепях описываются линейными уравнениями с постоянными коэффициентами.

Линейные цепи, содержащие хотя бы один элемент с переменными параметрами, называются линейными параметрическими цепями. Процессы в линейных параметрических цепях описываются линейными уравнениями с переменными коэффициентами.

В общем случае дифференциальное уравнение линейной цепи с сосредоточенными параметрами имеет следующий вид:

«v + av- --{-...+a,- + a,yf{t\ (1.61)

где у ~- искомая реакция цепи (ток или напряжение какой-либо ветви); а„, Oj, ,..,av- коэффициенты, определяемые параметрами пассивных элементов и коэффициентами управления управляемых источников. В дифференциальном уравнении линейной инвариантной во времени цепи эти коэффициенты постоянны, в дифференциальном уравнении линейной параметрической цепи, по крайней мере, один из них является функцией времени.

Правая часть уравнения (1.61) есть линейная комбинация функций, описывающих внонпюс воздействие на цепь х (t), и их производных. При вык.1юченипвсс.х источников она становится равной нулю.