оать как приближенное математическое описание {математическую модель) реальных процессов, имеюищх место в электрической цепи.

Определим период и частоту гармонической функции времени. Как известно, cos Э является периодической функцией 9 с периодом, равным 2я. Следовательно, изменение времени на период Т соответствует изменению фазы О на 2n:

(йГ = 2jt.

(2.4)

Используя (2.3) и (2.4), находим Т = 2п1щ f = (л!2л. Выражения (2.3), (2.4) позволяют определить также угловую час тоту гармонической функции по заданной частоте / или периоду Т

со = 2л!Т = 2nf.

(2.5)

Интервал времени, в котором значения гармонической функции положительны, например -(п/ (2й)) - (г/ю) < / < [я/ (2(й)1 - - (г)/ю), называется положительным полупериодом; интервал времени, в котором значения функции отрицательны, например я/ (2(й)1 - (if/w) < t < [Зл/ (2ю)1 - (if/w), - отрицательным. Совокупность значений функции на положительном полупериоде называется положительной, а совокупность значений функции на отрицательном полупериоде - отрицательной полуволной.

При построении временнйх диаграмм (графиков) гармонических функций обычно бывает удобным откладывать по оси абсцисс не время t, а пропорциональную ему величину att (рис. 2.2). В этом случае смещение точки = О относительно ближайшего максимума функции равно начальной фазе if. Если начало координат (точка

= 0) смещено вправо относительно ближайш(его максимума гармонической функции, то начальная фаза if является положительной, если влево - отрицательной. Если фазы 9i и двух гармонических функций ai (О == Ami cos {Ы + ifi) и а (t) =- А2 cos ((ot + гра) отличаются на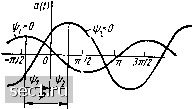

Рис 2.2. Гармонические функции с положительной и отрицательной начальными фазами

Ф = 9i - Ог = 11)1-г)2> О,

(2.6)

ТО говорят, что эти функции сдвинуты по фазе, причем функция Oi (t) опережает по фазе функцию а (t). Как видно из (2.6), разность фаз этих функций равна разности их начальных фаз и не зависит от времени Две гармонических функции одинаковой частоты совпадают по фазе, если разность их начальных фаз равна нулю; находятся в про-тивофазе, если ср =- ± п.

3 Зак

Среднее, средневыпрямленное и действующее значения гармонических токов и напряжений

Токи и напряжения цепи, изменяющиеся по гармоническому или другому периодическому закону, наряду с другими параметрами характеризуются средними за период, средневыпрямленными и действующими значениями.

Среднее значение периодической функ-цииа(Оза период Т определяется выражением

Кр= j a{t)dt. (2.7)

Интеграл, входящий в выражение (2.7), численно равен площади, заключенной между кривой а (i), осью времени и ординатами а {tg) и а (to + Т), причем площади, лежащие выше оси времени, берут со знаком плюс, а площади, лежащие под осью времени, - со знаком минус. Значение Ар не зависит от выбора момента времени to, поэтому при его определении можно полагать = О-

Среднее значение гармонической функции за период равно нулю, так как площадь, ограниченная положительной полуволной и осью времени, равна площади, ограниченной отрицательной полуволной и осью абсцисс (см. рис. 2.1, а). Таким образом, среднее значение гармонического тока или напряжения за период равно нулю.

Средневы прямленным значением периодического тока или напряжения называется среднее значение модуля соответствующей перодической функции а (t) за период:

4p.B=f \ I а (О На-

значение Лср.в пропорционально площади, ограниченной частью кривой \а (t) I и осью времени за период Т, и не зависит от выбора начального момента времени t.

Средневыпрямленное значение гармонического тока или напряжения равно среднему значению соответствующей гармонической функции а (t) на положительном полупериоде (см. рис. 2.1, б)

Я

(o-t-T 2(0 (О

ср.в= j Л„сов((й + г))сг=-1 j Arr,cos(iiit-\-dt.

\ 2(0 а )

Выполняя интегрирование и полагая 7 = 2л;/о), находим, что средневыпрямленное значение гармонического тока или напряжения в я/2 раз меньше его амплитуды

Лер.в= (2/я)Л„ = 0,637Л„. (2.8)

Действующим значением периодической функции а (t) называется среднеквадратическое значение этой функции за период Т:

/и+т

В соответствии с ГОСТ 1494-77 мгновенные значения токов и напряжений ветвей, токов источников тока и э. д. с. источников напряжения, являющихся гармоническими функциями времени, изображают строчными буквами: / = i (t), и = и (i), /= / (t), е= е {t)\ действующие значения этих величин - соответствующими прописными буквами /, и, J, Е и амплитудные значения - теми же прописными буквами с индексом т: /„, 1/, J„i, Е„- Размерность средних, сред-невыпрямленных и действующих значений гармонических токов и напряжений совпадает с размерностью соответствующих функций и, следовательно, с размерностью их амплитуд.

При протекании периодического тока i (/) через линейное сопротивление R в нем в соответствии с выражениями (1.12) и (2.9) за период Т выделяется энергия

W = Ij R[i{t)]4t = RPT. (2.10)

Выражение (2.10) совпадает с выражением для энергии, выделяющейся в сопротивлении при протекании через него постоянного тока / - / в течение времени Т (закон Джоуля- Ленца). Таким образом, действующее значение I периодического тока i (t) численно равно значению постоянного тока / , при протекании которого за время Т выделится такое же количество энергии, как и при протекании тока i (t). Аналогично можно определить и действующее значение U периодического напряжения и (t).

Действующее значение А гармонической функции а (t) в У2 раз меньше ее амплитуды:

4-1/ {А„соЦч,1+ЩЧ1 -

V 2Г

г<о--7- <о-1-т

j 4- cos 2 (ю + If) dt (с

0.707Л„. (2.11)

1/2-

Учитывая, что большинство потребителей реагируют на действующие, а не на максимальные (пиковые) значения токов и напряжений, при описании гармонических токов и напряжений принято указывать

3* 67