Комплексные числа и основные операции над ними

Символический метод комплексных амплитуд (комплексный метод, иногда, просто -символический метод) основан на представлении гармонических функций времени с помощью комплексных чисел или, точнее, на преобразовании исходных функций из временной области (области вещественного переменного t) в частотную область (область мнимого аргумента /ш).

Напомним, что комплексным числом А называется выражение

вида

А = А + jA"

(2.15)

где А и А"-действительные числа, называемые соответственно в е щ е с т-венной и мнимой частями комплексного числа; / = V - 1 - мнимая единица. Вещественную и мнимую части комплексного числа иногда обозначают: A = Re[A], А" = \т[А]. Выражение (2.15) - это а л г е б р а и ч е с к а я

форма записи комплексного числа.

1т А"

А Rf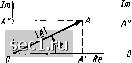

Рис. 2.3. К определению понятия комплексного числа

Комплексное число А изображается на комплексной плоскости в виде точки А, абсцисса которой равна А, а ордината - А" (рис. 2.3, а). Ось абсцисс, на которой откладывается вещественная часть комплексного числа, называется действительной (Re); ось ординат, на которой откладывается мнимая часть, -мнимой (Im),

Каждой точке А комплексной плоскости и, следовательно, каждому комплексному числу Л можно поставить в соответствие вектор А, проведенный из начала координат в точку А (рис, 2,3, б). Длину вектора, изображающего комплексное число, называют модулем этого числа

I Л1=У(Л)2 + (Л")2.

(2,16)

Угол а, образуемый вектором А с положительным направлением вещественной оси, называют аргументом комплексного числа:

А»

а= arctg

(2,17)

Положительное направление отсчета а - против часовой стрелки. Аргумент комплексного числа может иметь бесконечное множество значений, отличающихся друг от друга на 2nix, где п - целое число. Главное значение аргумента заключено в промежутке - я < а < л.

Как видно из рис. 2.3, б, вещественная А и мнимая Л" части комплексного числа А есть проекции вектора А на действительную и мнимую оси соответственно:

Л =Re [Л] = [Л] cos а; Л" = Im [Л] = Л sin а.

(2,18) 71

Подставляя соотношения (2.18) в выражение (2.15), можно перейти от алгебраической формы записи комплексного числа к тригонометрической:

.4.= Л cos«4-Л Л Isina. (2.19)

Далее, используя формулу Эйлера:

e--=cosa-f/"sina, (2.20)

где е - основание натурального логарифма, получаем показательную форму записи комплексного числа

A=\A\ei". (2.21)

Комплексные числа А = А + jA" = \А\е" и й = й + ]В" = jflle" считаются равными, если попарно равны их действительные н мнимые части: А = В, А" = В" (или, что то же самое, равны их модули j4i = s), а аргументы отличаются на 2пп, где п - целое число; - ("в ~ =Ь 2лп.

Два комплексных числа А = А jA" и А* = А - jA" называются с о-пряженными, если их действительные части равны, а мнимые отличаются только знаком. Точки на комплексной плоскости, изображающие сопряженные комплексные числа, симметричны относительно действительной оси (рис. 2.3,в). Модули сопряженных чисел равны, а главные значения их аргументов отличаются только знаком:

А-=\А1е"; Л = Ле--

Понятий «больше» и «меньше» для комплексных чисел не существует.

Арифметические операции над комплексными числами выполняются так же, как над обыкновенными двучленами, имея в виду, что == - 1. Операции сложении и вычитания удобнее выполнять, используя алгебраическую форму записи:

Л + й = (Л + М)-Ь (В+/В») (Л+й)+/(Л" + В»);

Л-в = (Л + /Л") - (5 + /й») = (Л - В) / (Л"-В").

Очевидно, что сумма двух сопряженных комплексных чисел Л =- Л + *

-(- /Л" и Л - А - /Л" представляет собой действительное число-

А + А = 2А. (2.22)

Умножение, деление и возведение в степень комплексных чисел удобнее проводить в показательной форме:

Л.В-.1Л!е".6е"« = Л 6 е

AIB = \А I е"/( В I е"«)= ( Л / В ) е ("-"в);

Л« = [Ле"т = М"е"". (2.23)

Из выражений (2.23) следует, что при умножении вектора Л = Ле"* на

действительное число т получается новый вектор, модуль которого в т раз больше модуля вектора Л:

тЛ = тЛе"*;

при умножении вектора А = lle" на вектор е*, модуль которого равен единице, получается новый вектор, повернутый относительно вектора Лна угол ijjg против часовой стрелки:

Л.е*=Ле("+*). (2.24)

Из (2.24) и формулы Эйлера следует также, что умножение вектора А = = \А\е" на вектор

/ = /sin (л/2) = e" (2,25)

равносильно повороту вектора А на угол п/2 против часовой стрелки:

Л=,Лe«/ = Иef"+>l. а умножение вектора А на вектор

/= -/sin (n/2)=e~"/ (2.26)

приводит к повороту вектора А на угол л/2 по часовой стрелке:

-4=Лe-/-/2 = Иef"-<">.

Наконец, умножение веКтора А па - 1 = cos (±л) + / sin (±я) = е*" равносильно изменению аргумента А на ±л: - 1-у4 = Ае" - lle""*"

Умножение и деление комплексных чисел можно производить также и в алгебраической форме:

А.В=(А +jA") (В+/В") = (Л В ~А» B) + i(A В- + А" В), ± A + jA" (А+jA") (В-jB") АВ+А"В" А" В-А В"

В B+jB" (В+jB") (В-jB") В2 Вр

причем при выполнении деления учитывается, что произведение двух комплекс-

но сопряженных чисел есть действительное число ВВ = (В + jB") (В - - /В") = (ВУ + {ВУ = В2.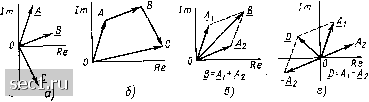

Рис. 2.4. Графическое определение суммы трех (а, б) и двух (в), а также разности двух (г) векторов

Суммирование комплексных чисел во многих случаях бывает удобно производить графически, используя правила действий над векторами. Вектор S, равный сумме векторов Л,, А, Лд,, может быть построен следующим образом: из начала координат строят вектор Л,, из его конца, как из начала координат, строят вектор А. из конца вектора А строят вектор Л 3 и т. д. Вектор, замыкающий ломаную линию, образованную из слагаемых векторов, представляет их сумму S. Так, вектор О, равный сумме векторов Л, В, и С (рис. 2.4, а, б), равен