замыкающей ОС = D ломаной линии ОАВС, построенной из векторов А = OA, В = АВ, С = ВС. Вектор В, равный сумме двух векторов А и Л,, - диагональ параллелограмма, построенного на сторонах Aj и А2 (рис. 2.4, в). Разность D = Ai - А может быть найдена как сумма векторов А и -А (рис. 2.4, г).

Комплексные изображения гармонических функций времени

Каждой гармонической функции времени а (t) можно поставить в соответствие комплексное число, называемое мгновенным или текущим комплексом гармонической функции:

а = Ат е <+* = л„ [cos И + •*)+/ sin И -f ф)], (2.27)

модуль которого равен амплитуде гармонической функции л, а аргумент - ее фазе 9 = (at + Как видно из выражения (2.27), ве. щественная часть мгновенного комплекса а равна исходной гармони, ческой функции

Re fa] = Am cos {at -f »))).

Пример 2.1. Мгновенные комплексы гармонического тока (j = SO-IO X Xcos [10*;-(-(я/3)] [А] и гармонического напряжения U2=l/2-100 cos [314 t -- ~(n/6)][B] равны соответственно. £i = 50 Ю еfи = = V2.100 e/t3i4<-(n/6)j

Вещественные части этих комплексов есть исходные гармонические функции:

Re [£,] = Re{50-10-3 cos [10" (n/3)l + /50-10-= sin[10e< +

+ (n/3)]} = 50- lO-* cos [10"/ + (л/3)] (i; Re(«J= Re {l/f.lOO cos f3I4/- (л/6)] +/I/2 100 sin [314/- - (ix/6)]} yi-lOO cos [314/ - (n/6)] = Uj.

Геометрически мгновенный комплекс a может быть представлен в виде вектора а = а(е"<\ длина которого а в определенном масштабе равна амплитуде А. соответствующей гармонической функции, а аргумент а (t) изменяется во времени по такому же закону, как и фаза гармонической функции а (t) = -fij;. Для того чтобы обеспечить этот закон изменения аргумента, вектор а должен вращаться в комп. лексной плоскости против часовой стрелки с угловой скоростью ю (рис. 2.5, а). в момент времени = о вектор а должен образовывать с положительным направлением вещественной оси угол ур, равный начальной фазе рассматриваемой гармонической функции. Как видно из рис. 2.5,а, проекция вектора а на вещественную ось в выбранном масштабе времени равна мгновенному значению исходной гармонической функции времени а (t) = Re la\.

Используя понятие комплексных сопряженных чисел и выражение (2.22), мгновенное значение гармонической функции а (t) можно оп-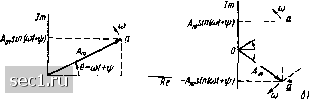

Рис, 2.5. К определению понятия мгновенного комплекса а гармонической функции

ределить так же, как полусумму мгновенного комплекса а = А е/<"+* и сопряженного ему комплексного числа а - Лте~/<+>:

а if) =(а+а*)/2= [Л„ е/ («"+*) + Л„ е-/ («"+*)J/2. (2.28)

Векторы а и а имеют одинаковую длину, противоположные по знаку начальные фазы и вращаются в комплексной плоскости в противоположных направлениях с одинаковой угловой скоростью ю (рис. 2.5, б). Проекции этих векторов на действительную ось равны

Re Ы = Re lal = Л„ cos (wif + гр),

а проекции на мнимую ось имеют различные знаки:

Im Ы = sin ((1) -f If), Im [a] = sin {mt -f яр).

Значение мгновенного комплекса а в момент времени == О называется комплексной амплитудой гармонической

функции времени а (О = Л cos (ю + гр):

Л„ = а,=о=Л„е/*. (2.29)

Из выражения (2.29) следует, что комплексная амплитуда гармонической функции времени а (i) = Л cos {(ot -f гр) представляет собой комплексное число, модуль которого равен амплитуде А „, рассматриваемой функции, а аргужнт - ее начальной фазе гз. Геожтрически комплексная амплитуда может быть представлена в виде неподвижного вектора, расположенного под угломк вещественной оси (рис. 2.6, а), длина которого в определен-

ном масштабе равна Л,..

Используя понятие комплексной амплитуды, выражение (2.27) для мгновенного комплекса а может быть преобразовано к следующему виду;

а = Л„ е/* е/» = Л„, е/®.

(2.30)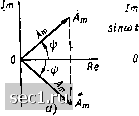

cascot Re

Рис. 2.6. К определению понятий комплексной амплитуды и оператора вращения е"

\gia>t

Вектор е*, называемый оператором вращения, имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью ю (рис. 2.6, б). Всякий неподвижный вектор, будучи умноженным на оператор вращения е/<, начинает вращаться в комплексной плоскости против часовой стрелки с

угловой скоростью (й.

В установившемся режиме токи и напряжения всех ветвей электрической цепи, находящейся под гармоническим воздействием, есть гармонические функции времени одной частоты. Каждому из токов и напряжений ветвей электрической цепи а (t) может быть поставлен в соответствие текущий комплекс а. Текущие комплексы, соответствующие токам и напряжениям различных ветвей, изображаются векторами, вращающимися с одинаковой угловой скоростью (неподвижными один относительно другого). Каждый из текущих комплексов токов и напряжений ветвей электрической цепи можно представить в виде произведения соответствующей комплексной амплитуды на оператор вращения e/< Очевидно, что оператор вращения является общим для мгновенных комплексов токов и напряжений всех ветвей и не несет информации о токах или напряжениях конкретных ветвей.

Токи и напряжения отдельных ветвей отличаются только амплитудами и начальными фазами, поэтому информация о них при известной частоте со содержится в соответствующих комплексных амплитудах. Зная амплитуды и начальные фазы токов или напряжений любой ветви, всегда можно однозначно найти их комплексные амплитуды и, обратно, по известной комплексной амплитуде можно однозначно установить амплитуду и начальную фазу исходного гармонического колебания.

Пример 2.2. Комплексная амплитуда гармонического пюка = 5 cos (10в; + -(- (я/6)] [А] есть /„1 = 5 е"®, а комплексная амплитуда гармонического напряжения Uj = 30 cos WtYB] равна 02 =• ЗОеЛ = зо.

Лри (О =5-10* рад/с комплексным амплитудам тока = l/2-ЗО- 10"*Х Хе~[AJ и э.д.с. = "1/2-10 [В] соответствуют мгновенные значения тока и э. д. с. «3 = "1/2-30 cos [(5-10*/ - п/4)] [мА]; е = v2-10 cos 5-10*/ [В].

Итак, установлено, что каждой гармонической функции времени а (t) можно единственным образом поставить в соответствие комплексное число Ajn (комплексную амплитуду), которое можно рассматривать как изображение этой гармонической функции в комплексной плоскости (по Г. Е. Пухову - комплексное изображение или К-изображение):

Л„ = К[а(01. (2.31)

Символом к будем обозначать операцию перехода от оригинала (исходной функции времени) к ее изображению в комплексной плоскости. Переход от гармонической функции времени а {t) к ее комплекс-