Выражения (2.56), (2.57) по структуре напоминают соотношения между мгновенными значениями напряжения и тока на зажимах линейного сопротивления (1.9), (1.10) и являются математической записью закона Ома в комплексной форме. В отличие от выражений (1.13), (1.16), (1.22), (1.23) уравнения (2.56), (2.57) являются алгебраическими.

Используя закон Ома в комплексной форме, каждому участку линейной электрической цепи, составленному из идеализированных пассивных элементов и имеющему два внешних вывода (см. рис. 2.7, а), в том числе любому идеализированному пассивному двухполюсному элементу, можно поставить в соответствие комплексную схему замещения, на которой рассматриваемый участок цепи представлен комплексным сопротивлением или проводимостью, а токи и напряжения на его зажимах - комплексными амплитудами (см. рис. 2.7, б) или комплексными действующими значениями (см. рис. 2.7, в).

Представляя все входящие в моделирующую цепь идеализированные пассивные элементы их комплексными схемами замещения, а токи и э. д. с. всех идеализированных источников - их комплексными амплитудами или комплексными действующими значениями, получаем комплексную схему замещения цепи (эквивалентную схему для комплексных амплитуд или эквивалентную схему для комплексных действующих значений). В отличие от этих схем замещения рассмотренные ранее эквивалентные схемы, на которых были изображены идеализированные двухполюсные элементы и указаны мгновенные значения токов i и напряжений и ветвей и идеализированных источников, будем называть эквивалентными схемами для мгновенных значений.

Таким образом, комплексная схема замещения цепн может быть получена из эквивалентной схемы для мгновенных значений заменой всех идеализированных пассивных двухполюсников их комплексными сопротивлениями (проводи-мостями) и всех токов и напряжений - их комплексными изображениями.

Мгновенные значения токов и напряжений различных ветвей электрической цепи связаны между собой линейными алгебраическими уравнениями баланса токов и напряжений, составляемыми на основании законов Кирхгофа. Учитывая, что суммированию гармонических функций времени соответствует суммирование их комплексных изображений, перейдем от законов Кирхгофа для мгновенных значений токов и напряжений к законам Кирхгофа для комплексных изображений токов и напряжений, называемых обычно законами Кирхгофа в комплексной форме.

Первый закон Кирхгофа в комплексной форме устанавливает связь между комплексными изображениями токов в каждом из узлов моделирующей цепи: сумма комплексных амплитуд (комплексных действующих значений) токов всех ветвей, подключенных к каждому из узлов электрической цепи, равна нулю:

S/„, = 0; 24=0. (2.58)

Здесь k - номер ветви, подключенной к рассматриваемому узлу.

Второй закон Кирхгофа в комплексной форме определяет связь между комплексными изображениями напряжений ветвей, входящих в произвольный контур электрической цепи: сумма комплексных амплитуд {комплексных действуюищх значений) напряжений всех ветвей, входяищх в любой контур моделирующей цепи, равна нулю:

Lu,nv=0; :t/v=0. (2.59)

Здесь V - номер ветви, входящей в рассматриваемый контур.

В ряде случаев удобно использовать другую формулировку второго закона Кирхгофа в комплексной форме: сумма комплексных изображений напряжений на всех элементах любого контура моделирующей цепи равна сумме комплексных изображений э.д.с, всех входящих в контур источников напряжения:

б„, = ;£,.; 56,= (2.60)

Здесь и mi, и с - комплексные изображения напряжений всех элементов контура, за исключением источников напряжения; Emj, Ej - комплексные изображения э. д. с. источников напряжения, действующих в рассматриваемом контуре.

В связи с тем что выражения (2.58)-(2.60) непосредственно вытекают из соотношений (1.37), (1.40) и (1.42), при суммировании комплексных изображений токов и напряжений ветвей электрической цепи в выражениях (2.58)-(2.60) сохраняются те же правила знаков, что и при суммировании мгновенных значений токов и напряжений.

Используя выражения для законов Ома и Кирхгофа в комплексной форме, можно составить систему уравнений электрического равновесия цепи для комплексных изображений токов и напряжений. В отличие от системы уравнений электрического равновесия, составленных для мгновенных значений токов и напряжений, уравнения электрического равновесия для комплексных изображений токов и напряжений являются алгебраическими. Решение таких уравнений намного проще, чем решение дифференциальных уравнений электрического равновесия, составленных для мгновенных значений токов и напряжений. Таким образом, с использованием комплексных схем замещения и составленных на их основании уравнений электрического равновесия цепи в комплексной форме анализ цепи переменного тока становится не сложнее анализа цепи постоянного тока и может производиться с использованием тех же приемов.

Общая схема применения метода комплексных амплитуд

Анализ цепей методом комплексных амплитуд содержит следующие этапы:

1) замена гармонических токов и напряжений всех ветвей их комплексными изображениями, а эквивалентной схемы цепи для мгновенных значений - комплексной схемой замещения;

2) составление уравнений электрического равновесия цепи для комплексных изображений токов и напряжений на основе законов Ома и Кирхгофа в комплексной форме;

3) решение системы уравнений электрического равновесия относительно комплексных изображений интересующих токов и напряжений;

4) переход от комплексных изображений токов и напряжений к их оригиналам.

§ 2.3. ИДЕАЛИЗИРОВАННЫЕ ПАССИВНЫЕ ЭЛЕМЕНТЫ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

Сопротивление

Пусть к идеализированному резистивному элементу сопротивлению (см. рис. 1.2) приложено напряжение, изменяющееся по гармоническому закону (рис. 2.9, а):

Ur - Y2Ur cos (мг + ipj.

(2.61)

Определим ток сопротивления Ir и его комплексное входное сопротивление Zr, а также построим диаграммы, характеризующие зависимость тока, напряжения и мгновенной мощности сопротивления от времени.

Связь между мгновенными значениями тока и напряжение линейного сопротивления определяется законом Ома (1.9). Подставляя (2.61) в (1.9), находим

iR = Ur/R = [V2Ur cos {wt+%)VR.

(2.62)

Из выражения (2.62) видно, что при гармоническом внешнем воздействии ток сопротивления является гармонической функцией времени той же частоты, что и напряжение (рис. 2.9, б). В общем случае гармонический ток через сопротивление

н j/Г/й cos (м/ + гз,). (2.63)

-71/2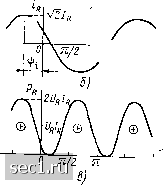

-ri/г

37i/Z 271 (Ot

Рис. 2.9. Временнйе диаграммы напряжения (а), тока (б) и мгновенной мощности (в) сопротивления

Сравнивая выражения (2.62) и (2.63), устанавливаем, что ток и напряжение линейного сопротивления совпадают по фазе