а действующие значения напряжения и тока связаны между собой соотношением /н = UrIR, подобным закону Ома для мгновенных значений. Мгновенная мощность сопротивления определяется произведением мгновенных значений напряжения Ыд и тока /д:

Pr = UrIr = 2UrIr cos {lat + yp).

Выражая- cos* {(ot + yp) через косинус двойного угла, получаем выражение для мгновенной мощности сопротивления

pr = (JrIr + UrIr cos 2 (wt + xp). (2.64)

Из выражения (2.64) следует, что мгновенная мощность сопротивления содержит две составляющие: постоянную, равную произведению действующих значений напряжения и тока, и переменную, изменяющуюся во времени по гармоническому закону с частотой, удвоенной по сравнению с частотой воздействующего напряжения (рис. 2.9, в). Максимальное значение мгновенной мощности сопротивления равно 2UrIr, а минимальное - нулю.

В связи с тем что ток и напряжение сопротивления имеют одинаковые начальные фазы, они одновременно достигают максимальных значений и одновременно проходят через нуль (рис. 2.9, а, б). Мгновенная мощность сопротивления всегда положительна, причем она обращается в нуль в точках, где ток и напряжение равны нулю, и достигает максимума в моменты времени, когда токи напряжение максимальны по абсолютному значению.

Среднее значение мощности сопротивления за период называется активной мощностью и равно произведению действующих значений напряжения и тока:

PA = P,~\PRdt== -[\ f cos2(a) + 4)]d=«/«. о о

Активная мощность численно равна постоянной составляющей мгновенной мощности и характеризует среднюю за период скорость потребления сопротивлением энергии от источника.

Комплексные ток и напряжение сопротивления /д = /де/*( = IJR /ij) и (/д = {Уде*» имеют одинаковые аргументы и отличаются по модулю в /?раз. На комплексной плоскости (Jr и /д изображаются векторами, которые совпадают по направлению и отличаются только масштабом (рис. 2.10, а).

Рис. 2.10. Векторные диаграммы для тока и напряжения (а), комплексного сопротивления (б) и комплексной проводимости (в) сопротивления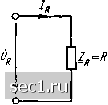

Комплексное сопротивление 2д идеализированного резистивного элемента - сопротивления равно отношению комплексных действующих значений напряжения и тока:

Zn = (JrHr = R. (2.65)

Представляя комплексное сопротивление Zr в показательной и алгебраической формах

Рис. 2.11. Комплекс-

Zr.= гц-Гц-\-\Хц (2.66) ная схема замещения

- участка цепи, содер-

и сравнивая (2.65) с (2.66), устанавливаем, что жащего сопротивле-модуль комплексного сопротивления равен "не

Zr == UrIIr = R, его аргумент срд = - if; = = О и что комплексное входное сопротивление Zr идеализированного резистивного элемента сопротивления содержит только вещественную составляющую: Лд = R, Хц = 0.

На комплексной плоскости Zr изображается вектором, направленным вдоль вещественной оси (рис. 2.10, б). Комплексная проводимость сопротивления Yr = 1/Zh = 1/? также изображается вектором, направление которого совпадает с направлением положительной вещественной полуоси (рис. 2.10, в).

Комплексная схема замещения сопротивления (рис. 2.11) имеет такой же вид, как и эквивалентная схема для мгновенных значений (см. рис. 1.2), и отличается от нее только тем, что .мгновенные значения тока Ir и напряжения Ur заменены их комплексными изображениями

Ir и 0.

Емкость

Рассмотрим емкость (см. рис. 1.5), к которой приложено напряжение, изменяющееся по гармоническому закону:

Uc = VWcCOS {(Ot + u)-

Используя выражение (1.13), найдем

du„

Jc=C-- = -~ii,CV2 Uc sin (Ш =

= /2"(йШсС05((1)-Ь i?„-f я/2). (2.67)

Как видно из (2.67), ток емкости изменяется по гармоническому закону

ic = У"21с cos (Ы -f ypi),

причем начальная фаза тока на п/2 больше начальной фазы напряжения: ipi = Фи + 2. т. е. ток емкости опережает по фазе напряжение на 90° (рис. 2.12, а).

Действующее значение тока емкости пропорционально действующему значению напряжения: 1с = utCUc-

Мгновенная мощность емкости рс при гармоническом воздействии изменяется по гармоническому закону с частотой в два раза большей частоты воздействующего напряжения (рис. 2.12, б):

Рс - Ucic \V~2Uc cos + г1:„)] [У21с cos (со + + "/2)1 = -2UcIc cos (wH-ilu) sin ((й/+-ф„)= -UcIc sin 2 (м/ + (2.68)

Как видно из временных диаграмм, в течение половины периода изменения мощности ток и напряжение емкости имеют одинаковый знак (емкость заряжается), при этом мгновенная мощность емкости положительна. В течение второй половины периода емкость отдает запасенную энергию (разряжается), при этом ток и напряжение емкости имеют различные знаки, а мгновенная мощность емкости отрицательна. Среднее значение мощности емкости за период {активная мощность) равно нулю:

pcdtO. (2.69)

ЗЛ/Z 2Я (jot

Энергия Wc, запасенная в емкости, определяется в соответствии с выражением (1.18), приложенным к ней напряжением:

Шс-=С«/2 = Cfycos2(cDi-f = Cfyg[l+cos2(u) + Tl3j]/2.

(2.70)

Из выражения (2.70) видно, что энергия емкости содержит две составляющие: переменную и постоянную, причем переменная составляющая энергии изменяется во времени по гармоническому закону с частотой, равной 2(й (рис. 2.12, в). Энергия емкости достигает максимального значения в те моменты времени, когда напряжение на емкости максимально по абсолютному значению; при уменьшении (по абсолютному значению) напряжения на емкости запасенная в ней энергия уменьшается и становится равной нулю в моменты времени, когда напряжение на емкости равно нулю. Таким образом, емкость периодически обменивается энергией с остальной частью цепи, причем энергия, запасенная в емкости, является неотрицательной величиной. Емкость не содержит внутренних источников энергии и поэтому в процессе разрядки не может отдать больше энергии, чем она получила от остальной части цепи в процессе зарядки.

Рис. 2.12. Временные диаграммы напряжения, тока (а), мощности (б) и энергии (в) емкости