жения на индуктивности U, которые определяют длину сторон тре-/гольника напряжений, связаны соотношением

г. е. действующее значение напряжения на входе цепи не равно алгеб-)аической сумме действующих значений напряжений на элементах 1епи.

Пример 2.3. Найдем комплексное входное сопротивление и ток последователь-юй RL-цепи (рис. 2.18, а), к зажимам которой прилоокено напряжение и =

= "1/2-50 cos (6,28 10*/+ 60"), В неопределим напряжения на элементах цепи R = 5 кОм, L = 1 мГн).

Комплексное входное сопротивление цепи Z равно сумме комплексных сопротивлений входящих в нее элементов:

Z = /? + /(oZ. = (5 -I- / 6,28) 10 Ом.

Переходя от алгебраической формы записи к показательной

£=8.03е/°, кОм,

шределяем модуль комплексного входного сопротивления z = 8,03 кОм и его аргумент (f = 51,5°. Находим комплексный ток цепи

lUJZ- =6,23е/85°, мА

- 8,03.103е1

и комплексные напряжения на сопротивлении и индуктивности

(yj,-./?/:5-103.6,23.10-3e«-° = 31,2e85 В;

()i = /a)Z./ = 6,28.106.1-10-3e°6,2310-3e-5°.39,le*-*, В.

Мгновенные значения соответствующих величин

(• = 1/2.6,23.10-3 cos (6,28.106 / + 8,5°), Л;

u,-=.y2.3l,2cos (6,28.10» / + 8,5°), В;

и--=У2.39,1 cos (6,28.108/+98,5°), в.

Последовательная /?С-цепь

Рассмотрим последовательную НС-цепъ (рис. 2.19, а), к зажимам которой приложено напряжение «, изменяющееся по гармоническому закону. Найдем комплексный ток цепи и ее комплексное входное сопротивление.

Переходя к комплексной схеме замещения цепи (рис. 2.19, б) и используя законы Ома и Кирхгофа в комплексной форме, составляем систему уравнений электрического равновесия цепи:

6 = f>Rf (Ус; VrZrIr,

i = jrtc, UcZcic, (2.90)

где Zr = R к Zc = V (/юС) - комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему уравнений (2.90) относительно комплексного действующего значения искомого тока, получаем

i=UKZji + Zc)U/Z.

(2.91)

Здесь 2 = £д + Zc - комплексное входное сопротивление рассматриваемой цепи, которое равно сумме комплексных сопротивлений последовательно включенных идеализированных элементов. Комплексная схема замещения цепи, соответствующая уравнению (2.91), приведена на рис. 2.19, в. Выразим комплексное сопротивление цепи Z через параметры входящих в цепь элементов: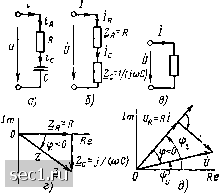

71/2

%i/{j<oc))i

ZZjZcR~-il{ii>C) = = ze/f, (2.92)

Рис 2 19. Схемы и векторные диаграммы последовательной /?С-цепи

где Z = [1/(«С)Р;

Ф = -arctg[l/(a)i?C)l.

Как видно из выражения (2.92), при конечных значениях а, R vl С угол ф лежит в пределах -jt/2<C ф < О, т. е. входное сопротивление цепи имеет резистивно-емкостной характер. Векторная диаграмма для комплексного входного сопротивления цепи приведена на рис. 2.19, г.

Подставляя (2.92) в (2.91), окончательно получаем

г 1 ?-Ь(1/(а)С)]

.g/{*u-f arcfg[l/((0C)]} (2.93)

Из выражения (2.93) видно, что ток / опережает приложенное напряжение и по фазе на угол ф. Совмещенная векторная диаграмма для тока и напряжений /?С-цепи приведена на рис. 2.19, д.

Последовательная iLC-цепь

Рассмотрим последовательную iLC-цепь (рис. 2.20, а), находящуюся под гармоническим воздействием, комплексная схема замещения которой приведена на рис. 2.20, б. Используя законы Ома и Кирх-

гофа в комплексной форме, составим систему уравнений электрического равновесия цепи

UUr-tUl+Uc, UlZlIu

/=/«-4=/с; Uc = Zcic; (2.94)

где Zh = i?; Zl = /wL; Zc = 1/ (/юС) - комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (2.94) относительно тока /, получаем

/ = V!{Zr Zl + Zc) = UIZ. (2.95)

Здесь Z- комплексное входное сопротивление последовательной iLC-цепи, равное сумме комплексных сопротивлений входящих в

1 Zfi=R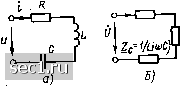

if<0

<p-0

Рис, 2.20. Схемы и векторные диаграммы для сопротивлений последовательной RLC-цепи

цепь элементов, которое определяется только параметрами входящих в цепь элементов и частотой вненшего воздействия:

Z=Zr+Z,+Zc = R + j [coL - 1 /((йС)]. (2.96)

Переходя от алгебраической формы записи Z к показательной, находим модуль и аргумент комплексного входного сопротивления:

2VWTbrWcW\ Ф - arctg """ . (2.97)

Из выражений (2,97) следует, что характер входного сопротивления цепи зависит от соотношения между мнимыми составлякщими комплексного входного сопротивления емкости Хс --l/((i)C) и индуктивности Хь - mL. При д;> \хс\ входное сопротивление цепи

iaK. 565