имеет резистивно-индуктивный характер (О < ф < я/2). Векторная диаграмма, построенная на основании уравнения (2.96) и иллюстрирующая данный случай, представлена на рис. 2.20, г (для большей наглядности векторы Zi, н изображены немного смещенными один относительно другого). Если лгг, < \хс\, то входное сопротивление цепи имеет резистивно-емкостной характер (-я/2 < ф < 0) (рис. 2.20, д). При Xl = \хс \ мнимые составляющие входного сопротивления емкости Хс и индуктивности Хь взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер (ф = = 0) (рис. 2.20, е).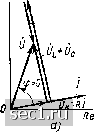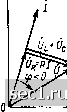

Рис. 2.21. Векторные диаграммы для тока и напряжений последовательной CL-цепи

Используя уравнение (2.95), можно по известному напряжению, приложенному к внешним зажимам цепи, найти ток и наоборот. Векторные диаграммы для тока и напряжений цепи, соответствующие различным соотношениям между мнимыми составляющими комплексного сопротивления емкости Хс и индуктивности Хь, приведены на рис. 2.21. Вектор Ur - RI, изображающий падение напряжения на сопротивлении, совпадает по направлению с вектором /; вектор С/ь = - jxtJ -- jtaLI повернут относительно / на 90° против часовой стрелки; вектор ilс - jxc - -jI/шС направлен противоположно вектору и. При Xi.> \хс\ (рис. 2.21, а) вектор Оь + Ос совпадает по направлению с вектором Ol, ток цепи отстает по фазе от напряжения (ф> 0). При х/, < д;с1 (рис. 2.21, б) вектор Ui, f Uc совпадает по направлению с вектором Uc, ток цепи опережает по фазе напряжение (ф<0). Если Xl, - \Хс\ (рис. 2.21, в), то вектор Oj, + Ос О, напряжение на зажимах цепи О равно напряжению на сопротивлении Or, ток цепи совпадает по фазе с приложенным напряжением (ф = 0).

Пример 2.4. Определим комплексное входное сопротивление и комплексный ток последовательной RLC-цепи (см. рис. 2.20, а) с параметрами L==80MKrH, С - 500 пФ, R - 100 Ом, к зажимам которой при.южено напряжение и --- У2-10 cos О)/, В, д.1я частот w, 2.5-10", <0j = 8-10« н oig -- 5- 1П« рад/с.

Комплексное входное сопротивление цепи (2 96) равно ti/MMe комплексных сопротивлений входящих в нее алементоо Подставляя в (,2.96) параметры элементов

цепи, находим комплексное сопротивление цепи при интересующих значениях частоты внешнего воздействия:

Z \ = 100-/600 = 608,Зе -/««-З", Ом; 51ш-<о.= 100+/390 = 402,6е"*°, Ом; f 1<о=<о.-00 Ом-

Таким образом, при ю = входное сопротивление цепи имеет резистивно-емкостной характер: при at = (и - резистивно-индуктивный: при ш = 0)3 - чисто резистивный.

Используя закон Ома в комплексной форме (2.95), находим комплексный ток цепи:

Как и следовало ожидать, согласно характеру комплексного входного сопротивления цепи, при о) = o)j -- ток опережает напряжение по фазе на угол 80,5°; при о) - - ток отстает по фазе от напряжения на угол 75,6°; при ш - напряжение и ток совпадают по фазе.

Параллельная LC-цепь

Рассмотрим параллельную iLC-цепь (рис. 2.22, а), к зажимам которой приложено напряжение, изменяющееся по гармоническому закону. Комплексная схема замещения цепи, в которой идеализированные двухполюсные элементы представлены их комплексными проводимостями, изображена на рис. 2.22, б.

Используя законы Ома и Кирхгофа в комплексной форме, составим систему уравнений электрического равновесия цепи:

I = !h + Ic+U\ fcYcUc;

U = UjiUc = Ul; !l = Yl Ul; (2.98)

Здесь Yr = l/R; Y c = /шС; = 1/ (/wL) - комплексные проводимости входящих в цепь идеализированных пассивных элементов. Решая систему уравнений (2.98) относительно тока /, получаем

/ = (Yji -Н Ус + Yl)U YU, (2.99)

гдеУ = Yr + Y c -т Yl - комплексная проводимость параллельной RLC-nenn, равная сумме комплексных проводимостей входящих в цепь идеализированных элементов. Далее будет показано, что комплексная проводимость любого участка цепи, состоящего из произволь-

4* 99

Horo числа параллельно включенных ветвей, равна сумме комплексных проводимостей этих ветвей. Комплексная проводимость параллельной RLC-nem, как и комплексная проводимость любой линейной цепи, не зависит от амплитуды (действующего значения) и начальной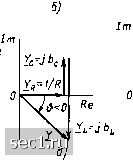

Рис 2.22. Схемы и векторные диаграммы для проводимостей параллельной

;?1С-цепи

фазы внешнего воздействия, а определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:

К = -1- Yc + Yl (l/R) Л j[мС- l/(u)L)].

(2.100)

Переходя от алгебраической формы записи к показательной (2.51), найдем модуль г/ и аргумент комплексной входной проводимости RLC-nena:

yl(l/Rf + [(oC-l/{(oL)f- 0-=arctg{/?[u)C-l/(ML)]. (2.101)

Анализ выражений (2.101) показывает, что характер входной проводимости, а следовательно, и характер входного сопротивления параллельной iLC-цепи зависят от соотношения между реактивными составляющими входной проводимости емкости be юС и индуктивности bL = -1/ (ю)- Когда Ьс> \Ьь\ (рис. 2.22, г), входная проводимость цепи имеет резистивно-емкостной характер (аргумент комплексной проводимости я/2> в О, поэтому аргумент комплексного входного сопротивления ср лежит в пределах -л/2<: ф < 0). При Ьс < lr.l (рис. 2.22, д) входная проводимость пени имеет резистивно-индуктивный характер, а при Ьс = \Ьь\ (рис. 2.22, е) реактивные составляющие входной проводимости емкости Ьс и индуктивности bi, взаимно компенсируются и входная проводимость цепи имеет чисто резистивный (вещественный) характер.