Уравнение (2.99) представляет собой математическую запись закона Ома в комплексной форме для параллельной /?1С-цепи. Комплексная схема замещения цепи, соответствующая этому выражению, приведена на рис. 2.22, в. Используя уравнение (2.99), можно по заданному напряжению определить ток, текущий через внешние за-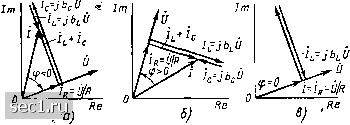

Рис. 2.23. Векторные диаграммы для токов и напряжения параллельной RLC-ntm при 6c>6i, (а), 6c<6i, {б), 6c=16i, (в)

жимы цепи, и, наоборот, по заданному току определить приложенное к цепи напряжение. Векторные диаграммы для токов и напряжения параллельной /?ЬС-цепи приведены на рис. 2.23.

Уравнения (2.98), описывающие процессы в параллельной ?1,С-цепи, подобны по структуре уравнениям электрического равновесия ранее рассмотренной последовательной /?1С-цепи (2.94) и могут быть получены из одного другое путем замены тока на напряжение, проводимости на сопротивление, емкости на индуктивность. Следовательно, параллельная и последовательная ?/,С-цепи являются дуальными. Векторные диаграммы дуальных цепей также могут быть получены из одних другие путем упомянутых замен.

§ 2.5. ЭНЕРГЕТИЧЕСКИЕ ПРОЦЕССЫ В ПРОСТЕЙШИХ ЦЕПЯХ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

Мгновенная мощность пассивного двухполюсника

Рассмотрим произвольный линейный двухполюсник, не содержащий источников энергии. Напряжение и ток на зажимах двухполюсника изменяются по гармоническому закону: и = Y2U cos {att -\- гр), i == 1/2/cos ((й + тр,) (рис. 2.24, а). Найдем мгновенную мощность двухполюсника

р ui = 2UI cos [Ш - ipu) cos (ю/ + гр) = UI cos ф + 17/ X

X cos {2Ы jfu l-ipO. (2.102)

где ф - -Ч"; - сдвиг фаз между напряжением и током.

Как видно из выражения (2.102), мгновенная мощность пассивного двухполюсника содержит постоянную составляющую ( со5ф, значение которой зависит от сдвига фаз между током и напряжением, и переменную составляющую Ul cos {2Ш + + «)> амплитуда которой UI не зависит от ф. Среднее значение мгновенной мощности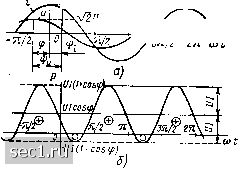

двухполюсника за период (активная мощность) численно равно постоянной составляющей мгновенной мощности

Рл=/со5ф. (2.103)

Анализ выражения (2.102) показывает, что особенности энергетических процессов в рассматриваемом двухполюснике полностью определяются характером его входного сопротивления.

Когда входное сопротивление двухполюсника имеет чисто резистивный характер (ф = 0), постоянная составляющая мгновенной мощности численно равна ампли-

туде переменной составляющей; мгновенная мощность изменяется от pmin = О до Ртах = 2UI, принимая только неотрицательные значения. Относительно внешних зажимов двухполюсник ведет себя подобно идеализированному пассивному элементу сопротивлению. В каждый момент времени двухполюсник только потребляет электрическую энергию от источника, необратимо преобразуя ее в другие виды энергии; обмен энергией между двухполюсником и источником энергии отсутствует. Если внутри рассматриваемого двухполюсника имеются энергоемкие элементы (емкости и индуктивности), то они могут обмениваться энергией только между собой, обмена же энергией между этими элементами и источником в установившемся режиме не происходит (более подробно это будет рассмотрено в гл. 3). Нетрудно убедиться, что при ф = 0 уравнение (2.102) вырождается в уравнение (2.64), поэтому временные диаграммы рассматриваемого двухполюсника полностью совпадают с временными диаграммами для сопротивления (см. рис. 2.9).

Если входное сопротивление двухполюсника имеет чисто реактивный характер ф = я/2, то постоянная составляющая мгновенной мощности равна нулю {Р = 0), мгновенная мощность изменяется по гармоническому закону с частотой, вдвое превышающей частоту внешнего воздействия. В данном случае двухполюсник ведет себя подобно емкости или индуктивности, в течение одной половины периода изменения мсщнссти запасая энергию от источника, в течение второй половины периода полностью отдавая ее источнику. При ф = --я/2 уравнение (2.102) может быть преобразовано к виду (2.75), а временное диаграммы совпадут с временньши диаграммами для индуктивности (см. рис. 2.15). Если ф = -я/2, уравнение (2.102) совпадает с (2.68), а временное диаграммы цепи имеют такой же вид, как и временное диаграммы для емкости (см. рис. 2.12).

Рис. 2.24. Временные диаграммы напряжения и тока (а), а также мощности (б) произвольного пассивного двухполюсника

Когда входное сопротивление двухполюсника имеет резистивно-емкостной или резистивно-индуктивный характер (0<ф<Я2), постоянная составляющая мгновенной мощности меньше амплитуды переменной составляющей, а мгновенная мощность двухполюсника изменяется от рщш = -UI (1 - cos ф) до pjx = UI (1 + cos ф), В течение большей части периода мгновенная мощность положительна, в остальной части периода - отрицательна (рис. 2.24, б). В двухполюснике имеет место как процесс запасания энергии, так и процесс необратимого преобразования ее в другие виды энергии, так как площадь, ограниченная участком кривой р (t) с положительными ординатами (численно равная энергии, потребляемой двухполюсником от источника), больше площади, ограниченной участком кривой р (t) с отрицательными ординатами (соответствующей энергии, возвращаемой цепью источнику). Характер энергетических процессов в цепи одинаков как при О < ф < я/2, так и при -я/2 < ф < О (временные диаграммы, приведенные на рис. 2.24, соответствуют О < ф < я/2).

Ни при каких значениях ц> энергия, отдаваемая пассивным двухполюсником во внешнюю по отношению к нему цепь, не может превышать энергию, потребляемую этим двухполюсником от внешней цепи.

Активная, реактивная, полная и комплексная мощности

Активная мощность, которая была определена как среднее значение мгновенной мощности за период, характеризует среднюю за период скорость поступления энергии в двухполюсник и численно равна постоянной составляющей мгновенной мощности (2.103). По знаку активной мощности можно судить о направлении передачи энергии: при Ра > О двухполюсник потребляет энергию, при Ра<.0 - отдает энергию остальной части цепи. Очевидно, что для двухполюсников, не содержащих источников энергии, активная мощность не может быть отрицательной.

Полной мощностью Ps называется величина, равная произведению действующих значений тока и напряжения на зажимах цепи:

Ps= UI. (2.104)

Полная мощность численно равна амплитуде переменной составляющей мгновенной мощности. Активная мощность двухполюсника может быть выражена через полную мощность:

Рл = Ps cos ц>. (2.105)

Из выражения (2.105) видно, что полная мощность есть максимально возможное значение активной мощности цепи, которое имеет место при ф - 0.

Комплексное число Р, модуль которого равен полной мощности цепи Ps, а аргумент -- углу сдвига фаз между током и напряжением ф, называется комплексной мощностью цепи

Ps = Paef<f. (2.106)