Переходя от показательной формы записи Pg к тригонометрической

Ps = PsC0S((, + jPgsmfp, (2.107)

устанавливаем, что вещественная часть комплексной мощности равна активной мощности цепи:

Re [Ps] = Ps cos ф = Pa. (2.108)

Мнимая часть комплексной мощности представляет собой так называемую реактивную мощность цепи

Im [Рд] = Ps sin ф = Pq. (2.109)

Реактивная мощность характеризует процессы обмена энергией между цепью и источником и численно равна максимальной скорости запасания энергии в цепи. В зависимости от знака угла ф реактивная мощность цепи может быть либо положительной, либо отрицательной. По знаку реактивной мощности, таким образом, можно судить о характере запасаемой энергии: при Pq> О энергия запасается в магнитном поле цепи, при Pq<.Q) - в электрическом. При = О в цепи

отсутствует обмен энергией с источником.

С учетом (2.108) и (2.109) выражение (2.107) можно записать следующим образом:

Р. Re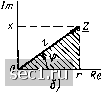

Рис. 2.25. Треугольники мощностей (а) и сопротивлений (б) произвольного пассивного двухполюсника

Ps-Pa + IPq. (2.110) Отсюда следует, что ком-

плексная мощность представляет собой комплексное число, вещественная часть которого равна активной мощности цепи Р, а мнимая - реактивной Pq.

Комплексному числу Ps можно поставить в соответствие вектор Ps, проекции которого на вещественную и мнимую оси равны, соответственно Ра и Pq (рис. 2.25, а). Прямоугольный треугольник с гипотенузой, равной Ps, и катетами и Pq называется треугольником мощностей. Из рисунка видно, что полная, активная и реактивная мощности связаны между собой соотношением

PhPX + Pb-

В связи с тем что треугольник мощностей цепи подобен треугольнику сопротивлений этой же цепи (рис. 2.25, б), комплексная мощность Ps и ее компоненты Ps, Ра, Pq могут быть выражены через комплексное сопротивление цепи Z и его компоненты г, г, х:

Ps=UI-= г; Pq Ps sin ф = Ulx/z = Рх; Р А-Ps cos и Ir/г-.Р г: Ps-=Ps-PzeKf.PZ, (2.111)

Найдем связь между комплексной мощностью и комплексными действующими значениями тока и напряжения на зажимах цепи. Подставляя в (2.106) выражения (2.104) и (2.48), находим

5 = {У/е= fyeu/е-*; =.0*1, (2.112)

где I 1е - число, комплексно сопряженное с / (комплексно сопряженный ток).

Таким образом, комплексная мощность цепи равна произведению комплексного напряжения цепи О на комплексно сопряженный

ток /.

Активная, реактивная, полная и комплексная мощности имеют одинаковую размерность [Дж/с]. Однако для того, чтобы подчеркнуть различный физический смысл, который вкладывается в эти понятия, единицам данных величин присвоены различные названия. Активная мощность, так же как и мгновенная мощность, выражается в ваттах [Вт], полная и комплексная мощности - в вольт-амперах [В • А], реактивная мощность - в вольт-амперах реактивных [вар].

Пример 2.5. Напрязкение и ток на зажимах произвольного двухполюсника из-, меняются по гармоническому закону:

и =- У2"-120 cos (314/+ 20°), В;

i = У2"-6,8 cos (314/ - 51°), мА.

Определим полную, активную, реактивную и комплексную мощности двухполюсника.

Комплексный ток !, комплексное напряжение U и угол сдвига фаз (р мео.сду током и напряжением на зажимах рассматриваемого двухполюсника:

/ /е*= 6,8. 10-3 е-°. Д;

(У:.(;е*"--120е-20°, В; ф = «-гг = 71°.

Подставляя эти величины в (2.104), (2.105), (2.109) и (2.112), находим искомые мощности:

P5 = t == 120.6,8.10-30,816 В. А; P = Wcos9 = 0,8l6cos71°-=0,266 Вт; Р5=-С 51пф =0,816sin71°r=0,772 вар;

Р5 = (;/= . 120е2°°6,8.10-зе°==0,816е° В-А.

В связи с тем что входное сопротивление цепи имеет резистивно-индуктивный характер (О < ф < л/2), реактивная мощность цепи положительна.

Баланс мощностей

Рассмотрим произвольную электрическую цепь, содержащую Идеальных источников напряжения, М идеальных источников тока и Я идеализированных пассивных элементов. Пусть - ток и

напряжение k-го элемента цепи. Из закона сохранения энергии следует, что сумма мгновенных мощностей всех элементов цепи в каждый момент времени равна нулю:

N + M + H +

2 л= 2 «й=о- (2.113)

/е = 1 *=1

Группируя члены, соответствующие идеализированным активным (Phnct) И идеализированным пассивным (рпочр) элементам, уравнение (2.113) можно преобразовать к виду

N+M Н

- 2 Ph"cT~ 2 i потр- (2.114)

Уравнение (2.114) называют уравнением (условием) баланса мгновенных мощностей. Принимая во внимание, что мгновенная мощность любого элемента характеризует скорость потребления энергии этим элементом (потребляемая мощность), а мгновенная мощность, взятая со знаком минус, характеризует скорость отдачи энергии этим элементом (отдаваемая мощность), условие •баланса мгновенных мощностей может быть сформулировано следующим образом: сумма мгновенных мощностей, отдаваемых всеми источниками, равна сумме мгновенных мощностей, потребляемых всеми приемниками энергии (необходимо иметь в виду, что потребляется и отдается не мощность, а электрическая энергия).

Можно показать, что условие, аналогичное (2.114), выполняется и для комплексных мощностей всех элементов;

N + M Н

- 2 М-ист= V Р5,„отр. (2.115)

Уравнение (2.115) называется уравнением (условием) баланса комплексных мощностей. Таким образом, сумма комплексных мощностей, отдаваемых всеми идеализированными активными элементами, равна сумме комплексных мощностей всех идеализированных пассивных элементов.

Для практических расчетов электрических цепей условие баланса мощностей удобно представить в следующей форме:

2 ч 2 " 2 "Ч- (2.116)

А = 1 к-1 /г=1 7

Левая часть выражения (2.116) представляет/собой алгебраическую сумму комплексных мощностей, отдаваемых врми активными элементами. Слагаемое вида Е/ есть произведение комплексного действующего значения э.д. с. источника напряжениз/на комплексно сопряжен-

иый ток этого источника; слагаемое вида равно произведению

комплексного напряжения на источнике тока на комплексно сопряженный ток этого источника. Слагаемые, состоящие в левой части выражения (2.116), берут со знаком плюс, если направления токов и напряжений источников выбраны в соответствии с рис. 2.26. В против-