Объединяя условия (2.120) и (2.122), находим, что наибольшее возможное значение активной мощности нагрузки Рд шах max соответст-

вует Z„ -~ Гц + /х„ = Л/ - fxi или Z„ = Z,-, где Z,- - величина, сопряженная с комплексным внутренним сопротивлением источника.

Таким образом, для согласования источника энергии с нагрузкой по критерию наибольшей активной мощности, передаваемой в нагрузку, сопротивление нагрузки должно быть величиной, комплексно сопряженной с внутренним сопротивлением источника. В частном случае, если

"а max max 1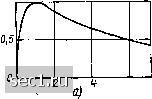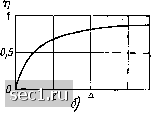

Рис. 2,28. Зависимость активной мощности нагрузки (а) и к. п. д.

(б) от вещегтвенпой составляющей сопротивления нагрузки г„

прн хв=-хг

внутреннее сопротивление источника имеет чисто резистивный характер (Zj - /j),to сопротивление нагрузки должно выбираться равным

в}!утреннему сопротивлению источника Z„ Z; - г,.

Коэффициент полезного действия цепи (см. рис. 2.27) равен отношению активной мощности, потребляемой нагрузкой Р v, к суммарной активной мощности, потребляемой в цепи: ц - - rj4 ir„P + пП rj (Гн + П).

Зависимость к. п. д. от резистивной составляющей сопротивления нагрузки показана на рис. 2.28, б. Из рисунка видно, что к. п. д. цепи монотонно возрастает с ростом rjri, приближаясь к = 1 при г„ -г-> оо.

Таким образом, для согласования источника с нагрузкой по критерию максимума к. п. д. необходимо, чтобы резистивная составляющая сопротивления нагрузки была намного больше резистивной составляющей внутреннего сопротивления источника (л,, > л,).

Рассмотренные критерии согласования источника энергии с нагрузкой являются несовместимыми, т. е. не могут выполняться одновременно. В частности, при согласовании источника с нагрузкой по критерию максимальной активной мощности, передаваемой в нагрузку, к. п. д. цепи будет равен 0,5. Очевидно, что мощные электроэнергетические системы не могут работать с к. п. д., при котором половина выработанной энергии теряется на внутреннем сопротивлении источника, поэтому обычно стремятся к достижению максимально возможного значения к. п. д., выбирая r,,/ Г;. Согласование по критерию максимальной активной мощност1, передаваемой в нагрузку, широко используется в маломощных радиоэлектронных устройствах.

когда независимо от потерь необходимо добиться выделения максимальной мощности сигнала в нагрузке.

Следует отметить, что приведенные рассуждения справедливы только для источников с конечным внутренним сопротивлением. Для источников с i?i = О или Gj - О г] - 1 при любом конечном значении резистивной составляющей сопротивления нагрузки, а выделяемая в нагрузке мощность неограниченно возрастает с уменьшением при питании от источника напряжения {1.26)1 или с увеличением [при питании от источника тока (1.27)1 г„.

§ 2.6. ПРЕОБРАЗОВАНИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Понятие об эквивалентных преобразованиях

Анализ процессов в электрических цепях во многих случаях может быть существенно упрощен за счет использования различных преобразований, в результате которых отдельные участки идеализированных цепей заменяются участками с более простой топологией или участками, более удобными для анализа.

Два участка идеализированной электрической цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения остальной части цепи не изменяются. Преобразования электрических цепей, в результате которых некоторые участки электрической цепи заменяются эквивалентными им участками, называются эквивалентными. Из определения эквивалентных участков следует, что они должны иметь одинаковое количество внешних выводов, причем в процессе эквивалентных преобразований токи этих выводов и напряжения между ними должны остг ваться неизменными.

Эквивалентные участки электрических цепей обладают свойствами симметричности (если цепь А эквивалентна цепи Б, то цепь Б эквивалентна цепи А), рефлексивности (цепь А является эквивалентной самой себе) и трапзистивности (если цепь А эквивалентна цепн Б, а цепь Б эквивалентна цепи В, то цепи А и В являются эквивалентными). Если эквивалентность двух участков электрической цепи выполняется при любых значениях внешних воздействий, то такие участки являются полностью эквивалент н ы м и. Различия между ними не могут быть установлены с помощью каких-либо измерений, проводимых на внешних выводах. Если эквивалентность двух участков выполняется только при определенном значении внешних воздействий, то такие участки являются частично эквивалентными (эквивалентными при заданных условиях). Так, два участка линейной электрической цепи, находящейся под гармоническим воздействием, могут быть либо полностью эквивалентными, либо частично при заданной частоте внешнего воздействия.

Эквивалентные преобразования электрических цепей основаны на эквивалентных (равносильных) преобразованиях соответствующих систем уравнений электрического равновесия. Каждое равносильное

преобразование системы уравнений электрического равновесия исходной цепи (приведение подобных членов, исключение неизвестных, замена переменных и т. д.) приводит к эквивалентному преобразованию моделирующей цепи. Соответственно изменяется и условное графическое изображение моделирующей цепи - схема цепи. На практике преобразования электрических цепей проводят без составления систем уравнений электрического равновесия, путем непосредственного преобразования схем по определенным правилам. Систему уравнений электрического равновесия цепи составляют для уже преобразованной цепи, схема которой имеет достаточно простой вид.

Рассмотрим правила преобразования цепей с последовательным и параллельным соединением элементов.

Участки цепей с последовательным соединением элементов

Рассмотрим неразветвленную электрическую цепь (рис. 2.29, а), содержащую N сопротивлений, М емкостей, К индуктивностей и v Неуправляемых источников напряжения (обобщенная -бдно-контурная цепь). Так как через все элементы цепи протекает один и тот же ток /, то уравнение электрического равновесия, состав-денное на основе второго закона Кирхгофа и компонентных уравнений, может быть записано в следующей форме:

Rii + ... + RN i + г idt + ...-{- г idt +

-OO -OO

+ 1г + ...-{-1к~и[ег + ...-е]. (2.124)

at dt

После приведения подобных членов (2.124) принимает вид

?эк+- J idt + L,~-=ue,,„ (2.125)

- оо

N , М , К V

где Рэк --= s л = s М э„ = s и, еэк = 2 Ci.

i=l эк j=i i=l i= 1

Уравнению (2.125) соответствует преобразованная цепь, схема которой изображена на рис. 2.29, б. Таким образом, ток и напряжение на зажимах обобщенной одноконтурной цепи не изменятся, если каждую из групп последовательно включенных однотипных элементов заменить одним эквивалентным элементом, параметр которого R, Cg, эк и вэк рассчитывается в соответствии с (2.125).

Из выражения (2.125) следует, что при последовательном включении сопротивлений, индуктивностей и источников напряжения параметры эквивалентного элемента R, Лэк " равны сумме паражтров последовательно включенных элементов соответствуюш,его типа. При этом суммирование э. д. с. источников напряжения производится ал-