гебраически, с учетом их знаков, которые определяются тем, совпадает или не совпадает направление э. д. с. с направлением обхода контура. Очевидно, что Rg„ и Ьз„ будут превышать сопротивление и индуктивность любого из последовательно включенных элементов. При последовательном соединении одинаковых сопротивлений R или индуктивностей L параметр эквивалентного элемента /?эк или Lg„ будет в N раз больше, чем параметр каждого из последовательно включенных элементов.

При последовательном включении емкостей значение величины, обратной Сэ„, определяется как сумма обратных значений всех последовательно включенных емкостей, причем эквивалентная емкость Сэ„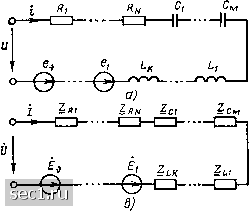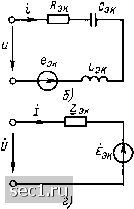

Рис 2.29. Преобразование участка цепи с последовательным соединением

элементов

меньше, чем любая из последовательно включенных емкостей. При последовательном включении одинаковых емкостей эквивалентная емкость Сэк в раз меньше каждой из последовательно включенных емкостей.

Если обобщенная одноконтурная цепь находится под гармоническим воздействием, то от эквивалентной схемы для мгновенных значений (рис. 2.29, а) удобнее перейти к эквивалентной схеме для комплексных действующих значений (рис. 2.29, в). Уравнение электрического равновесия такой цепи, составленное на основании закона Ома и второго закона Кирхгофа в комплексной форме, имеет следующий вид:

+ ZLK/ = -[£i + ... + -ev]. После преобразований получаем

Z,JU-E,„, (2.126)

i-Де Zen = 2 + I Zc- + i Zli; - s Ei.

Комплексная схема замещения цепи, соответствующая уравнению (2.126), приведена на рис. 2.29, г.

Таким образом, любой участок электрической цепи, представляющий собой последовательное соединение произвольного количества идеализированных неуправляемых источников напряжения и идеализированных пассивных двухполюсников, при гармоническом воздействии может быть заменен ветвью, содержащей один источник напряжения, э.д.с. которого равна алгебраической сумме э.д.с. всех последовательно включенных источников, и один пассивный двухполюсник, комплексное сопротивление которого равно сумме комплексных сопротивлений всех последовательно включенных пассивных двухполюсников.

Участки цепей с параллельным соединением элементов

Пусть электрическая цепь (рис. 2.30, а) состоит из параллельно соединенных N сопротивлений, М емкостей, К индуктивностей и v неуправляемых источников тока (обобщенная двухузловая цепь). Все элементы цепи находятся под одним и тем же напряжением и, поэтому уравнение электрического равновесия, составленное на основании первого закона Кирхгофа, может быть записано в форме

i-u .... + -±-и + С, + ... + С, + Ri Rf dt dt

] + J «rf-[/i + ...+/vl. (2.127)

- 00 -CXI

После приведения подобных членов получаем

i=-« + C,«- + --l г udt-U,, (2.128)

- оо

где ь~ = s D-; ак s Ci\ .- =2 2 il-

Уравнению (2.128) соответствует преобразованная цепь, схема которой приведена на рис. 2.30, () Видно, что ток и напряжение на зажимах обобщенной двухузловой цепи не изменятся, если каждую из групп [[араллельно включенных однотипных :*лементов заменить одним эквивалентным элементом, параметры которою R, Сэк, Lbk и /ак рассчитываются в соответствии с (2.128).

Из выражения (2.128) следует, что при паралмльном включении емкостей и источников тока параметры эквивалентного элемента С,и, /ви равны сумме параметров паршыельно включенных .мементов соответствующего типа. При этом суммирование токов источников тока производится алгебраически с учетом нх знаков, определяемых ориентацией источников относительно узла, для которого составляется уравнение (2.127). Очевидно, что превышает по значению любую из параллельно включенных емкосгсй Си См- ТТри параллельном соединении N одинаковых емкостей Сди - NC.

При параллельном включении сопротивлений или индуктивностей значения величин, обратных /?эк и L, будут определяться как сумма (кратных значений этих сопротивлений или индуктивностей. Значения Яэк и /.эк будут меньше, чем сопротивление или индуктивность любого из параллельно включенных элементов соответствующего типа. При параллельном включении одинаковых сопротивлений R или индуктивностей L, Ran = РШ, а /.э„ = UN.

J-,---- о 1

6J г;

Рис, 2 30. Преобразоваине участка цепи с параллельным соединением

элементов

Для рассмотрения параметров обобщенной двухузловой цепи при гармоническом воздействии воспользуемся комплексной схемой замещения этой цепи (рис. 2.30,в). Уравнение электрического равновесия цепи в комплексной форме может быть записано следующим образом:

+ Пк/-[л + ...--л] или / = п,-Уз„, (2.129)

где - s Yr, + 2 Yc, Ч- s Уи\ /э„ = 2 J г-

- 1=1- » = 1 - 1=1- /= 1

Комплексная схема замещения цепи, соответствующая уравнению (2.129), изображена на рис. 2.30, г.

Таким образом, любой участок электрической цепи, представляющей собой параллельное соединение произвольного количества идеализированных пассивных двухполюсников, может быть заменен одним пассивным двухполюсником, комплексная проводимость которого Yk {авна сумме комплексных проводимостей всех параллельно включенных двухполюсников. Произвольное количество параллельно включенных идеализированных источников тока может быть заменено Одним источником, комплексное действующее значение тока которого Jk равно сумме комплексных действующих значений токов всех параллельно включенных источников.

Переходя в (2.129) от комплексных проводимостей к комплексным сопротивлениям, найдем эквивалентное комплексное входное сопро-